お絵描き特殊相対性理論

本書では，特殊相対性理論を時空図と運動量図を用いて議論しました。 グラフ用紙に時空図を描き，時空図から読み取った数値と 特殊相対論からの数値を比較しながら進めていきます。 本書はAmazonでのみ購入可能です。

本書ででてくる図は，もともとすべてグラフ用紙に描いています。 それを以下に掲載します。

• 第1章

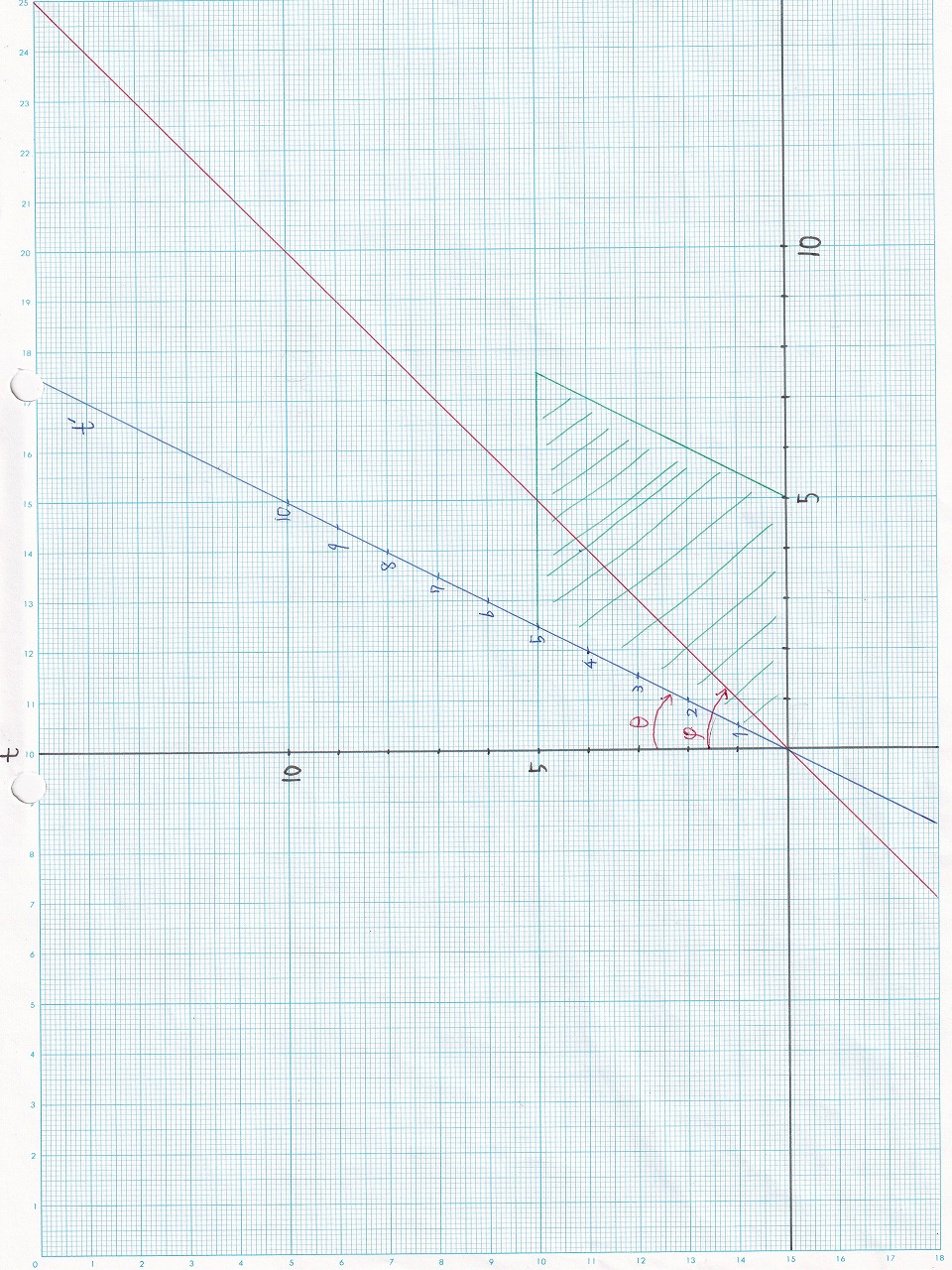  図1.2	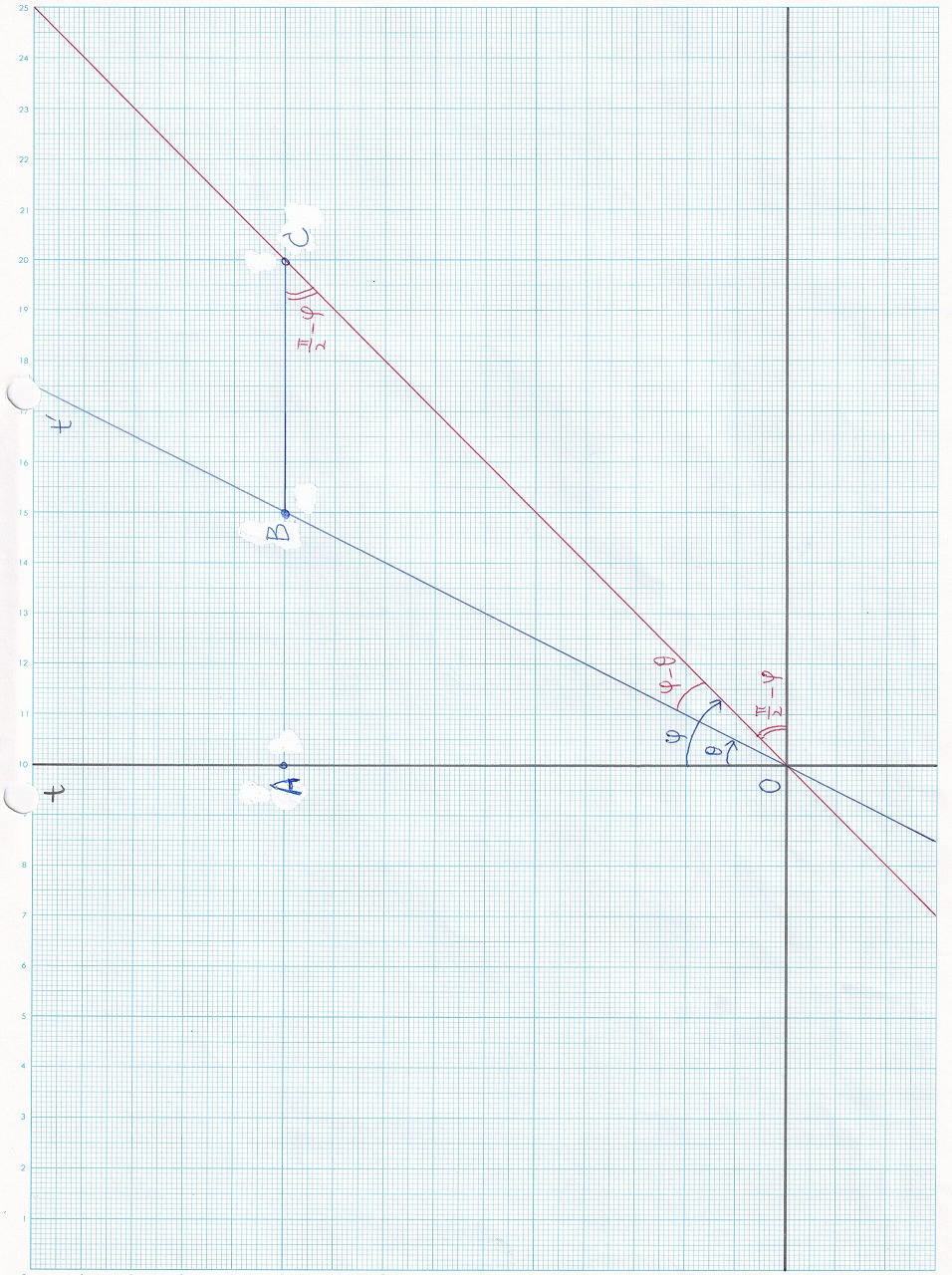図1.8
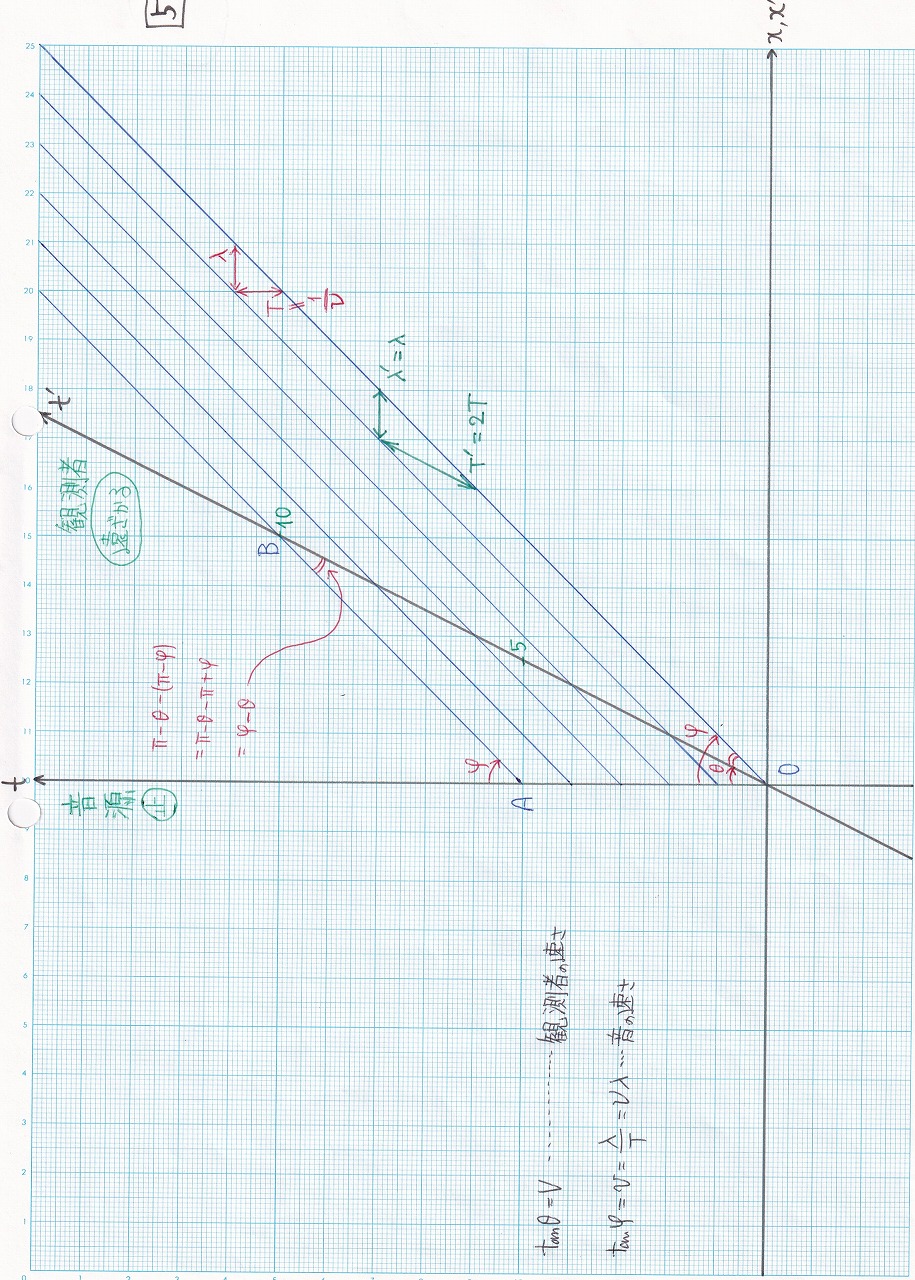  図1.10	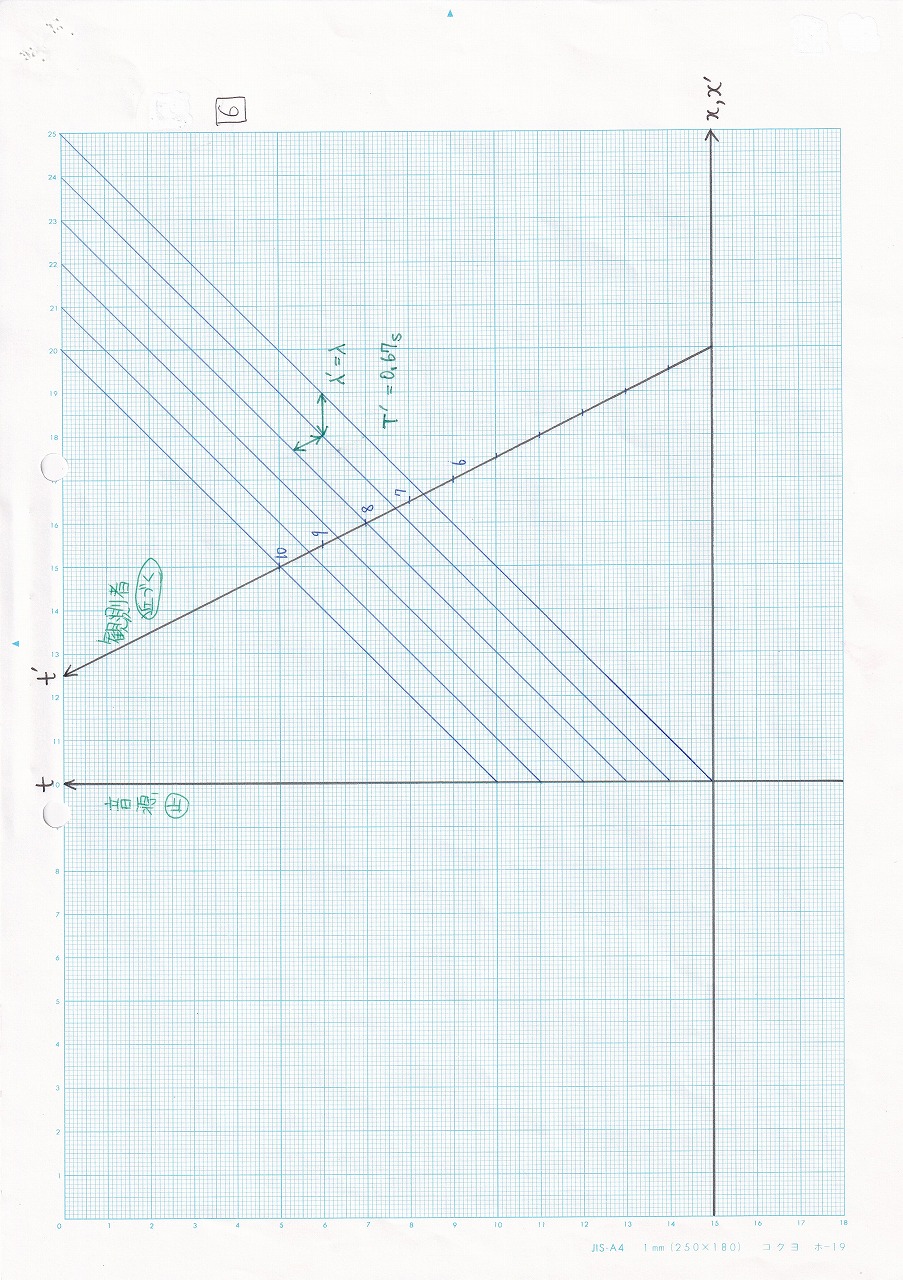図1.11
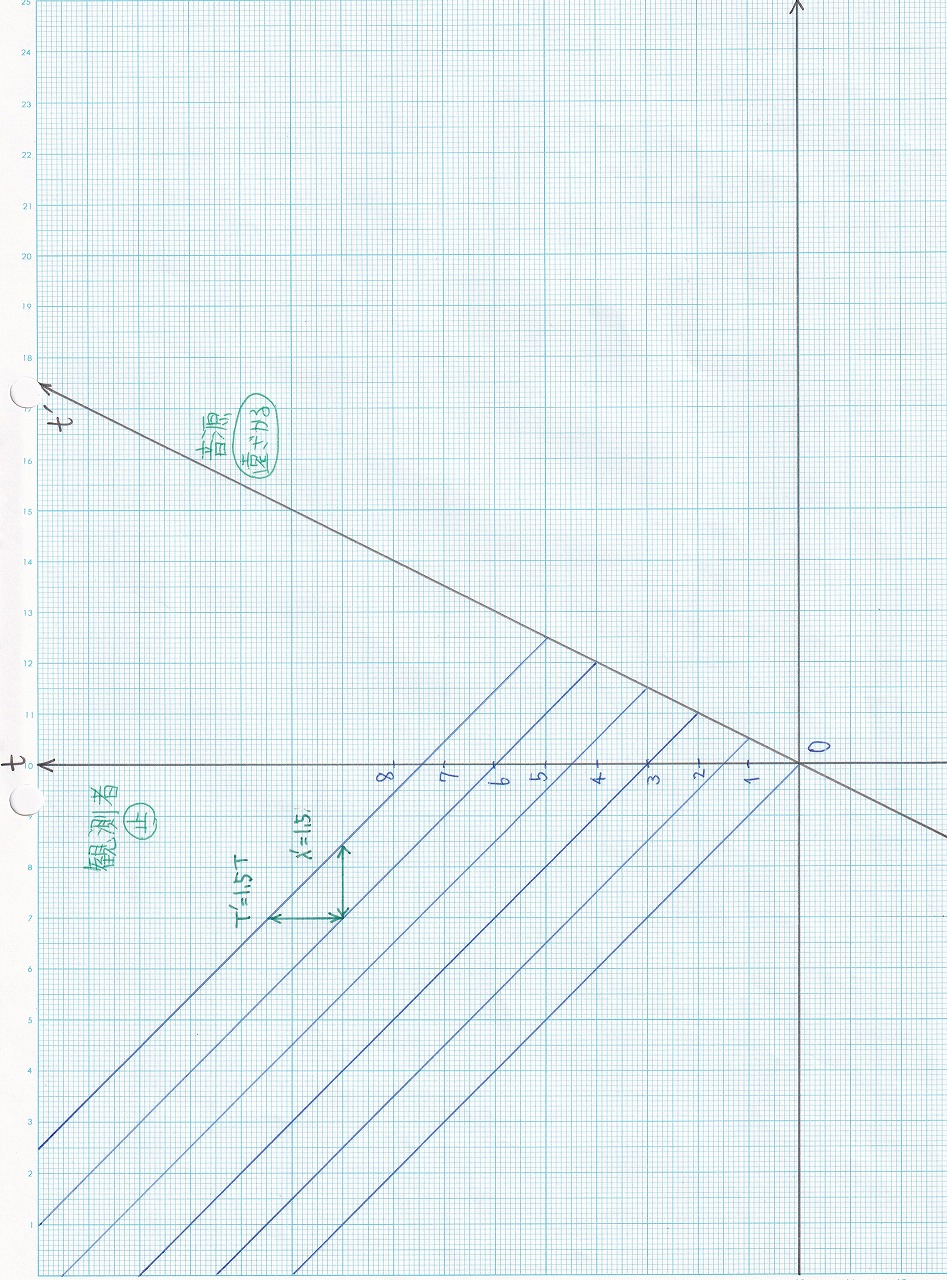  図1.12	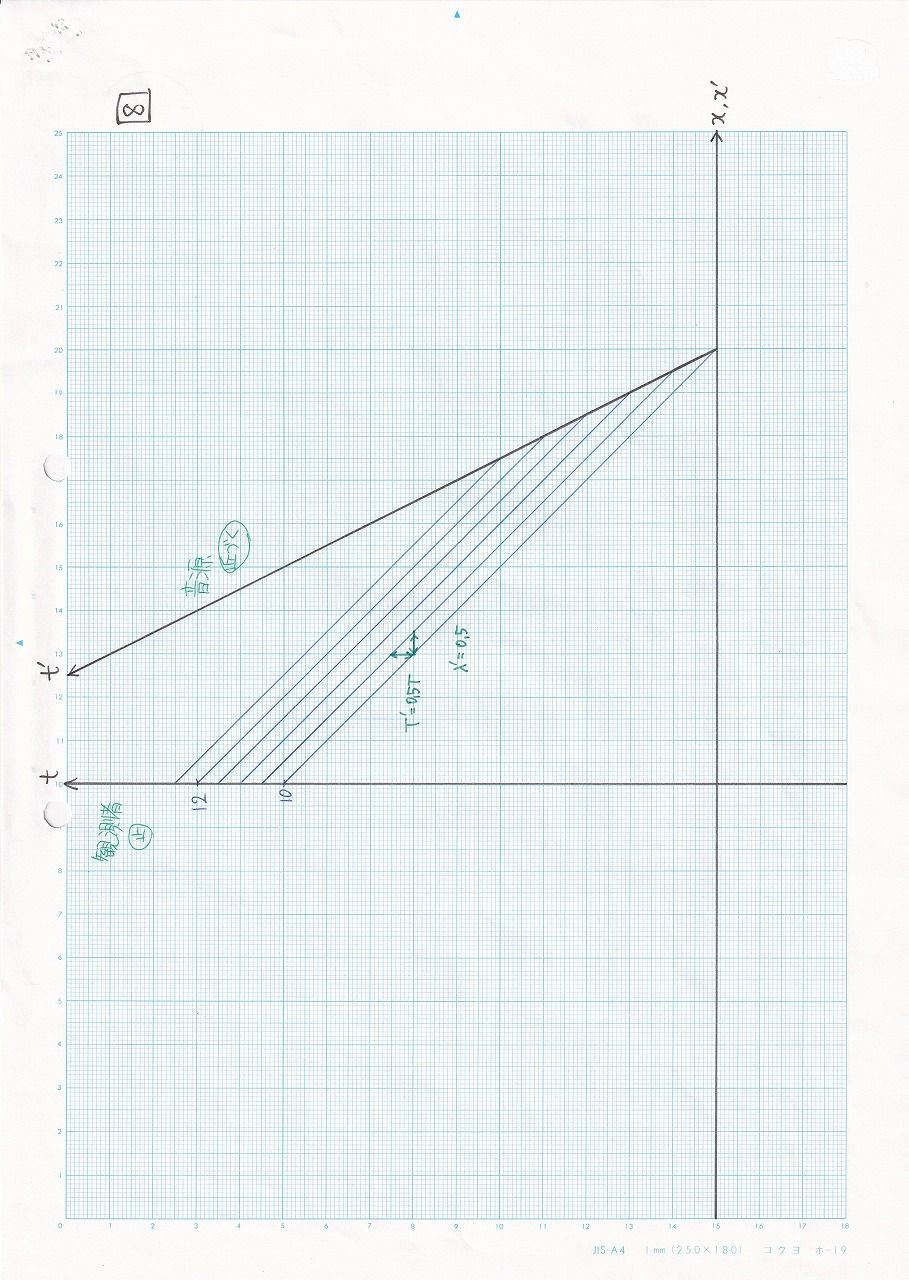図1.13

  ---

• 第3章

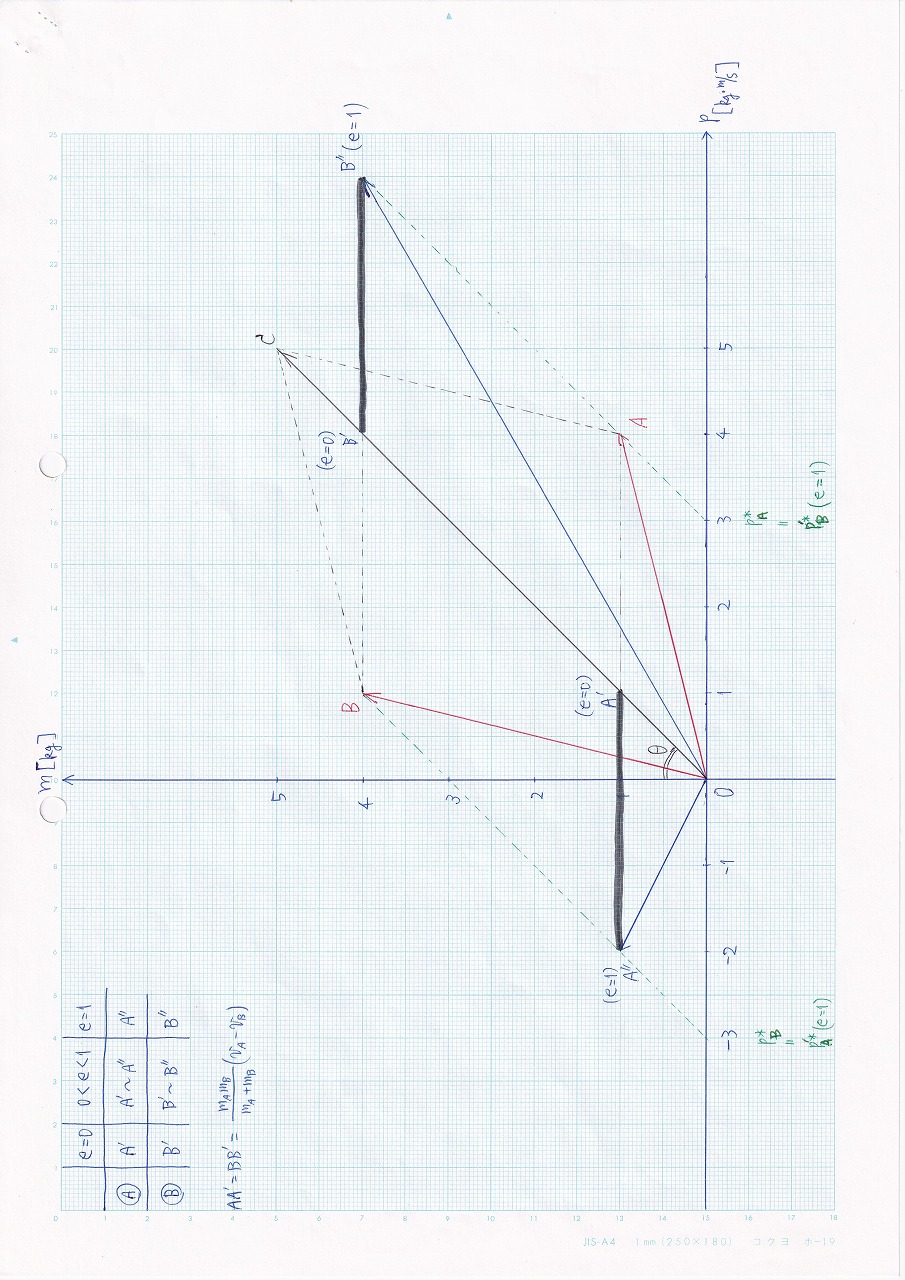  図3.6～3.9	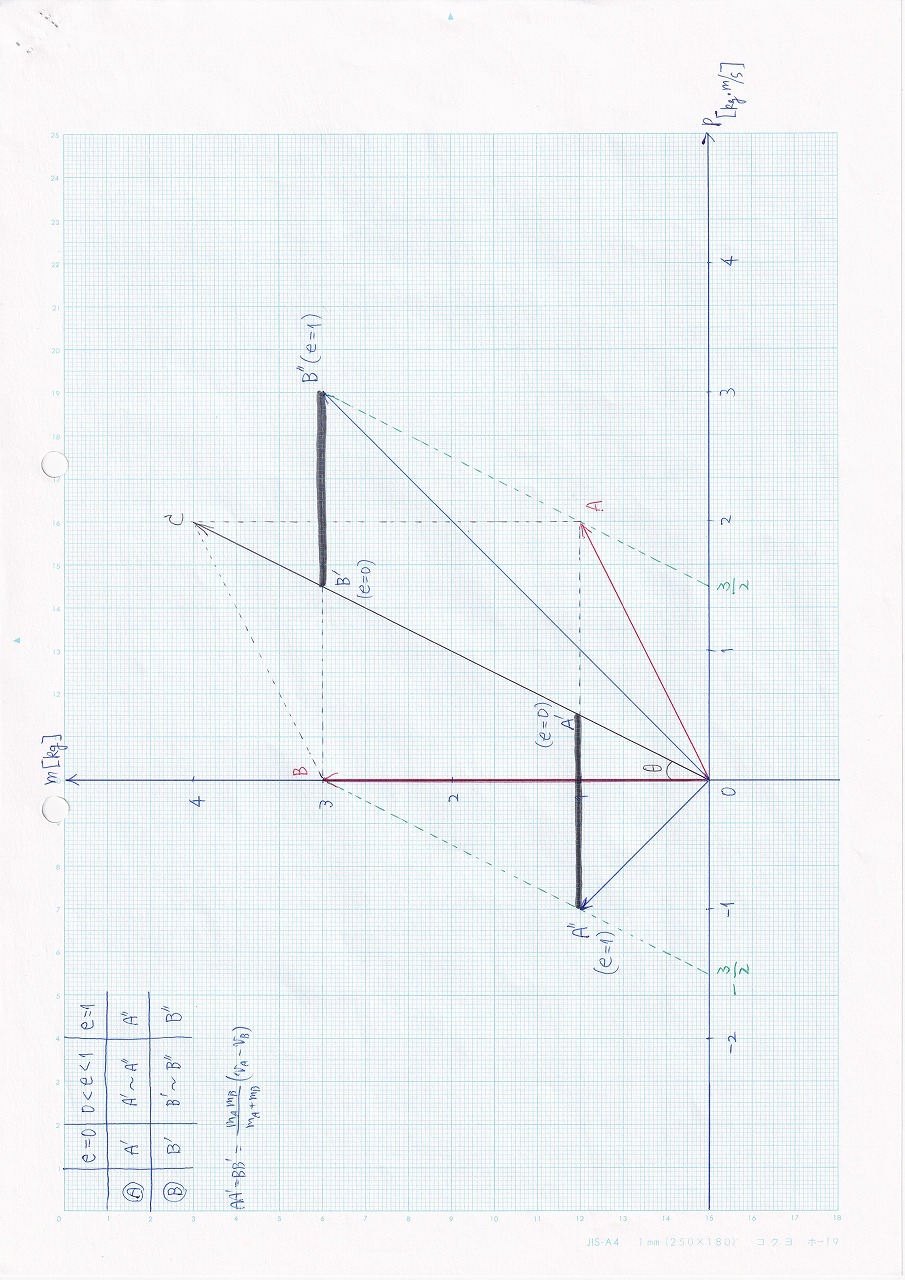図3.10～3.11
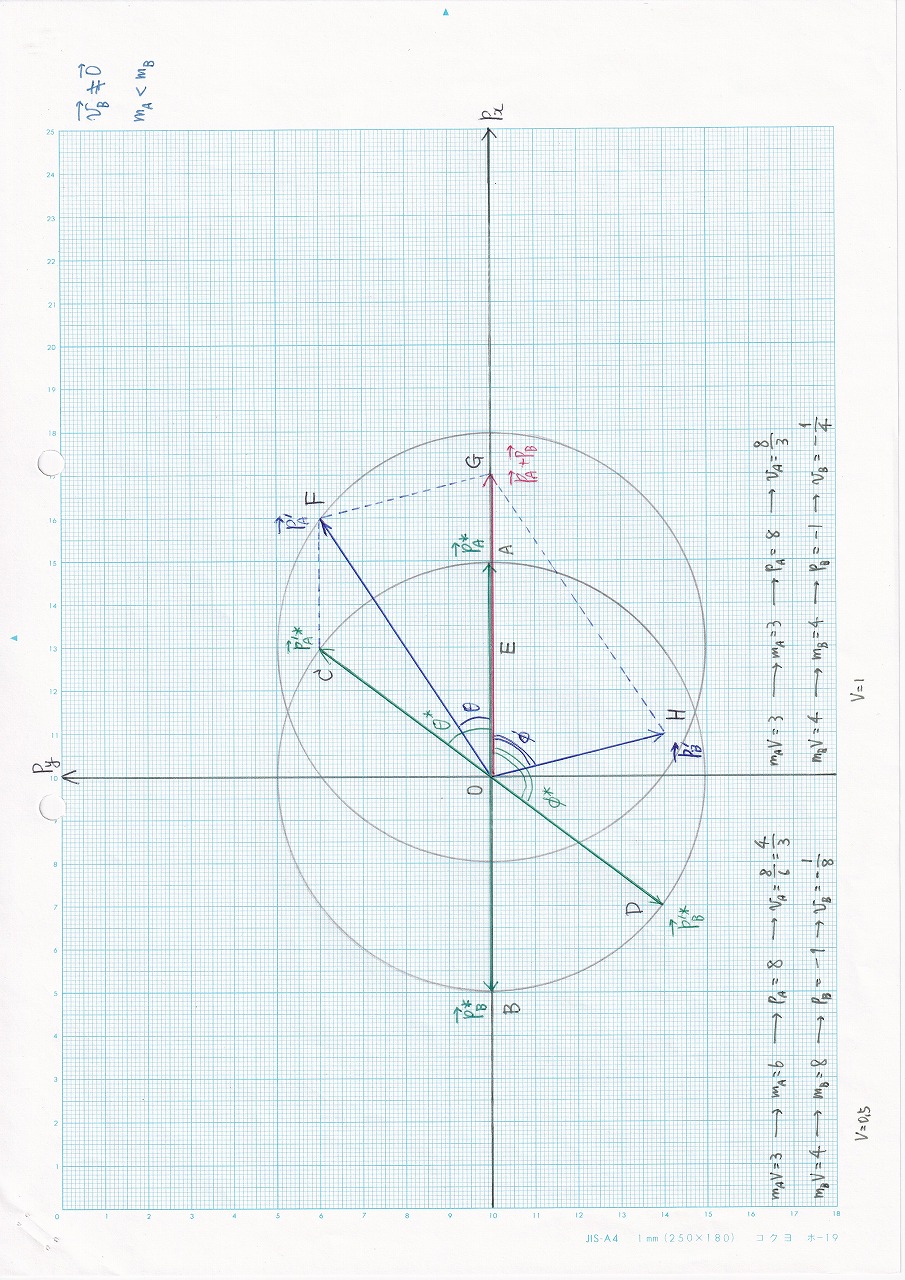  図3.15：vB ≠ 0，mA<mB	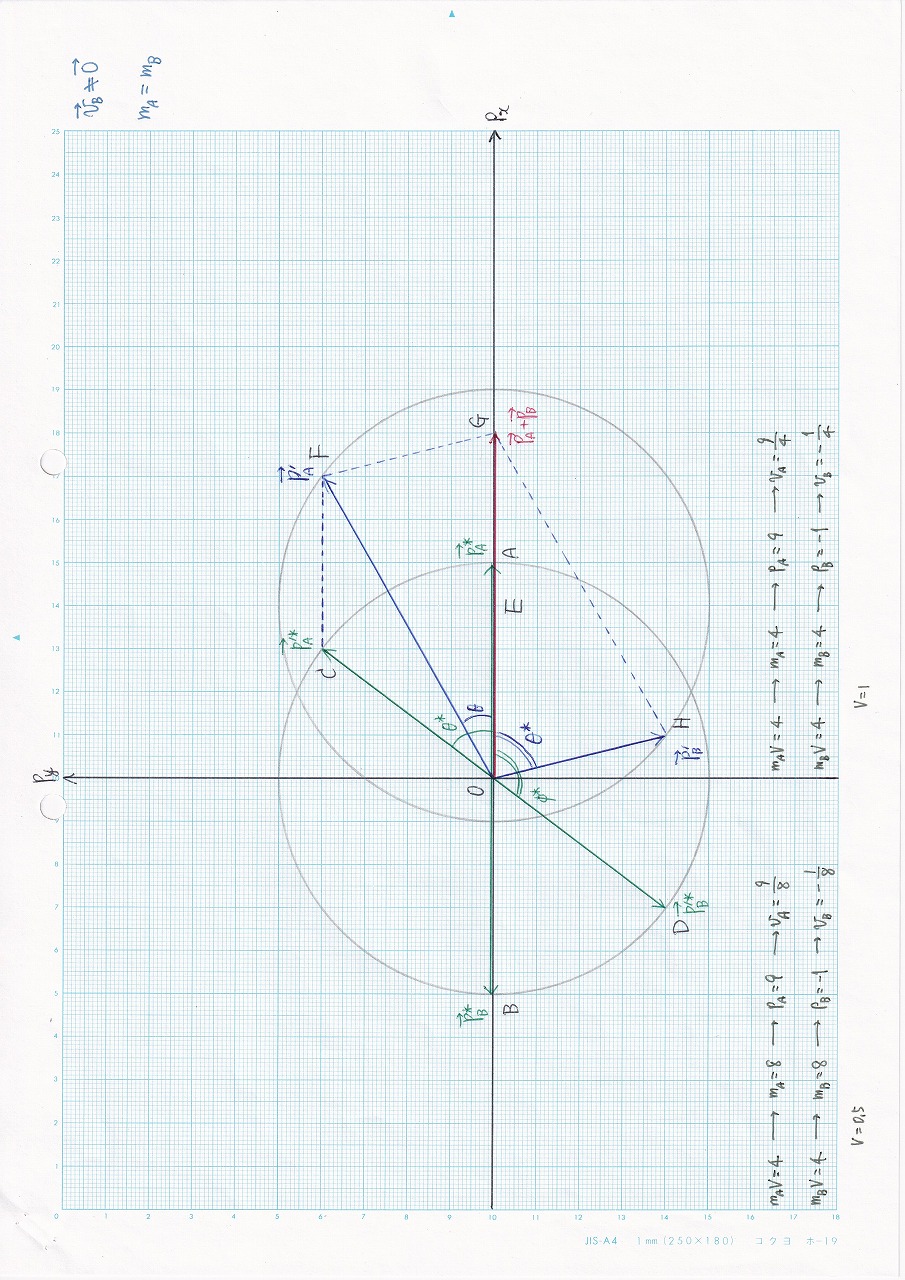なし：vB ≠ 0，mA = mB
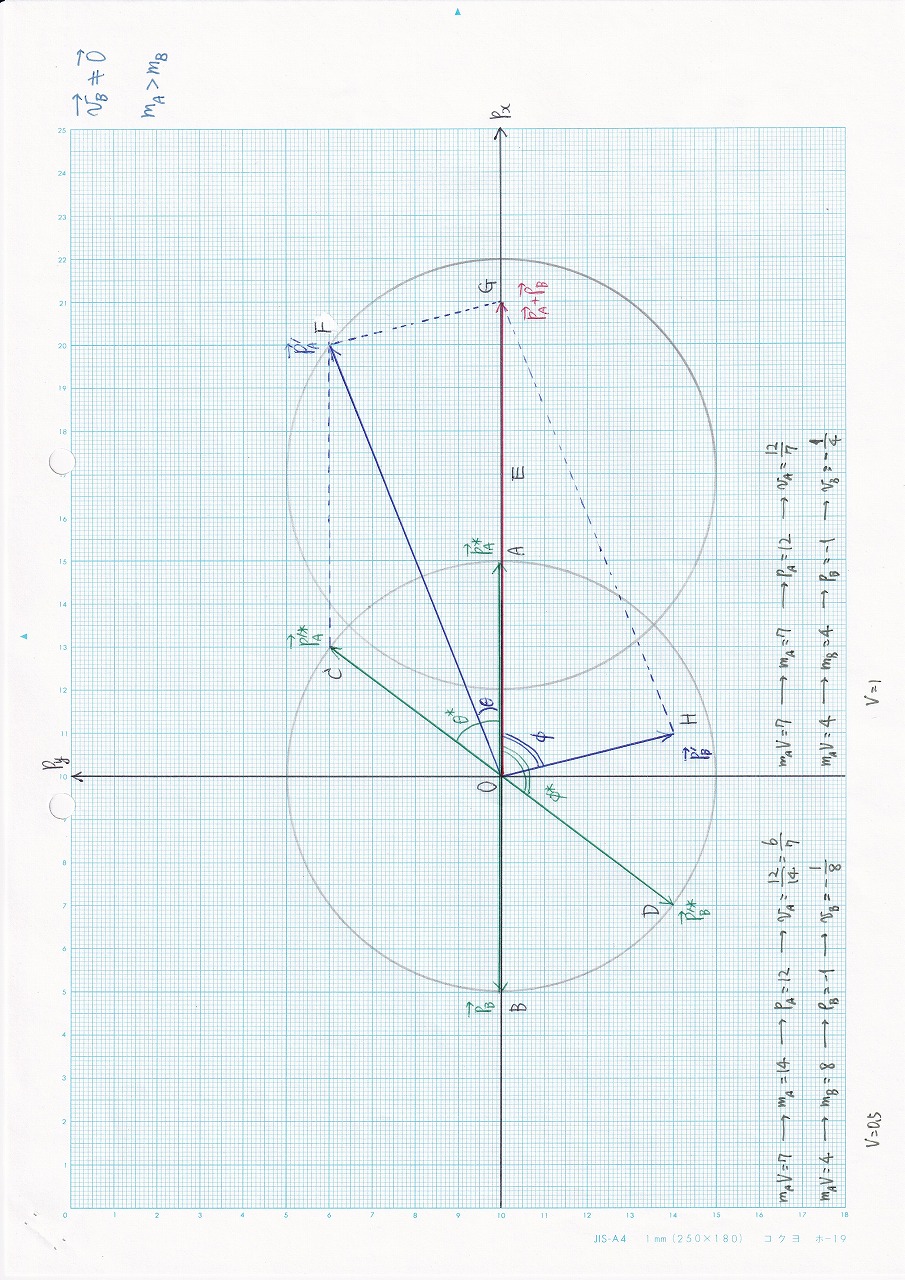  なし：vB ≠ 0，mA>mB	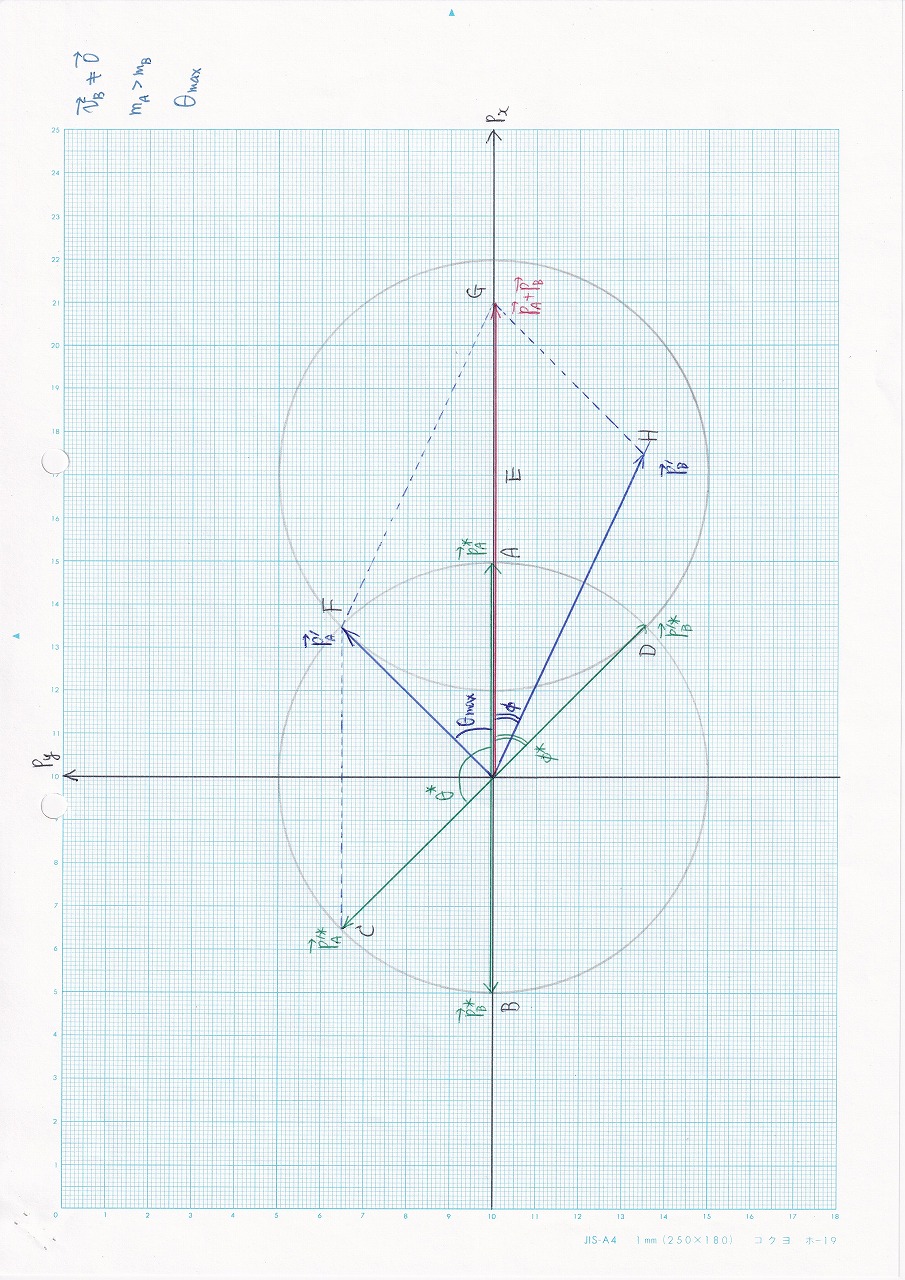なし：vB ≠ 0，mA>mB，θmax
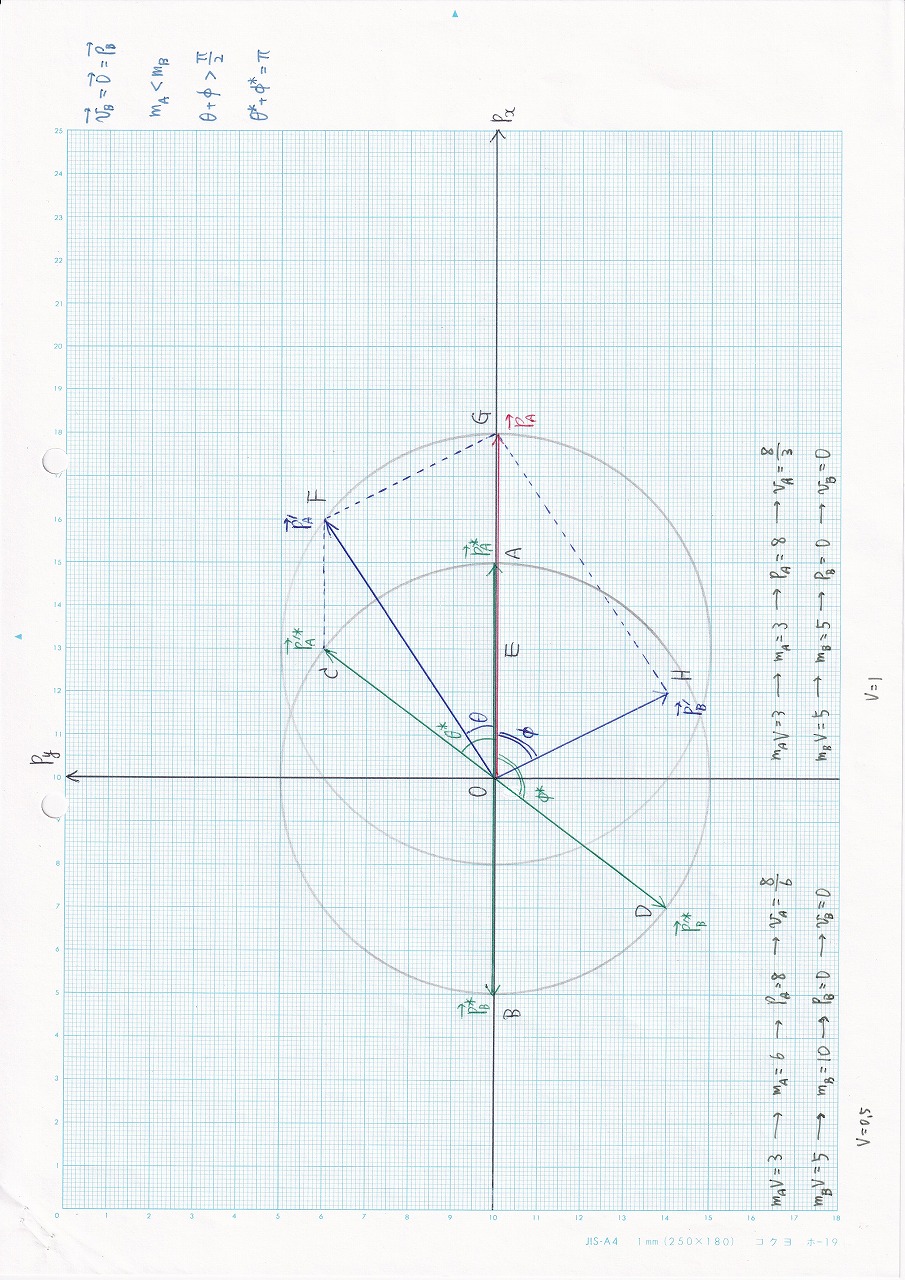  図3.16：vB= 0，mA<mB	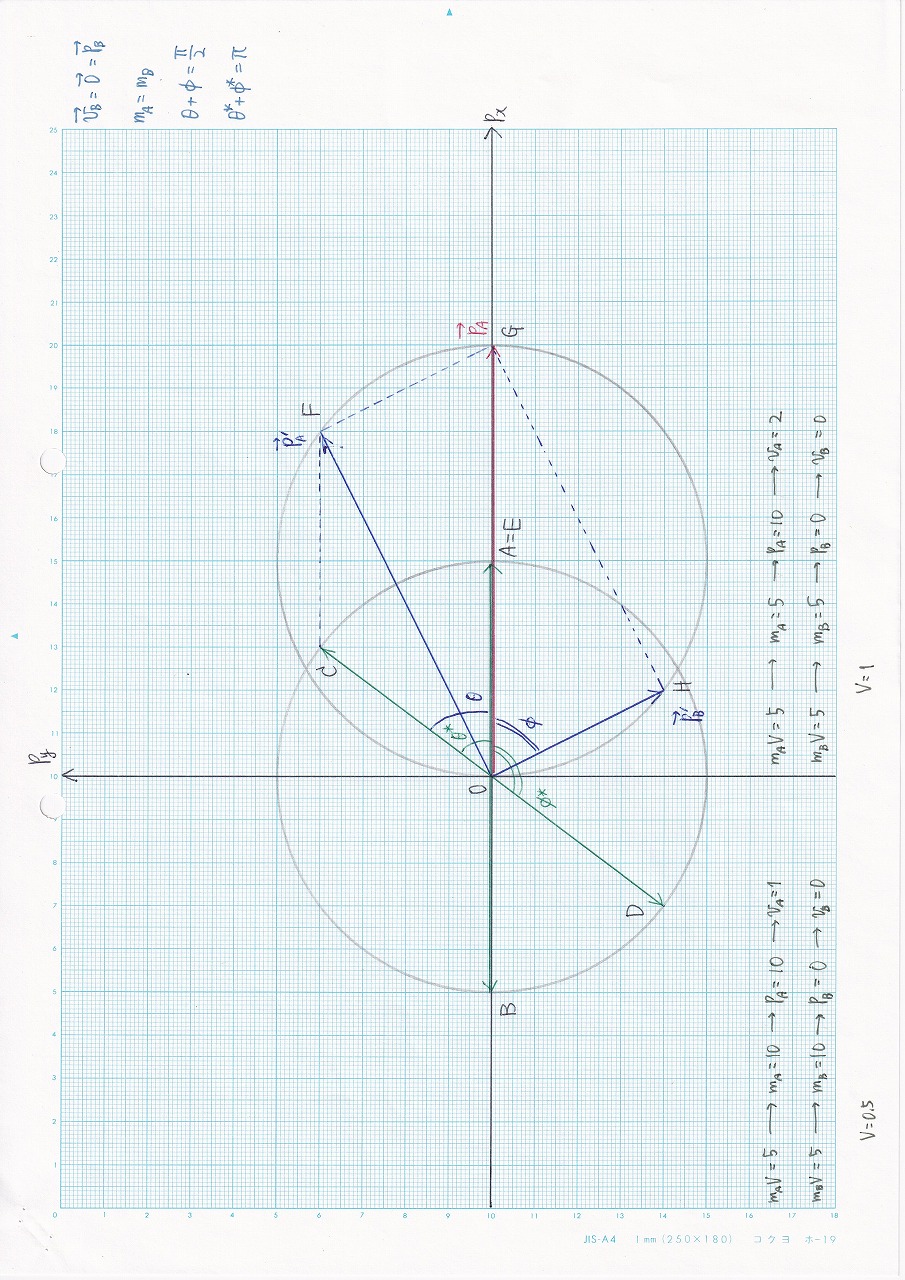図3.19：vB= 0，mA=mB
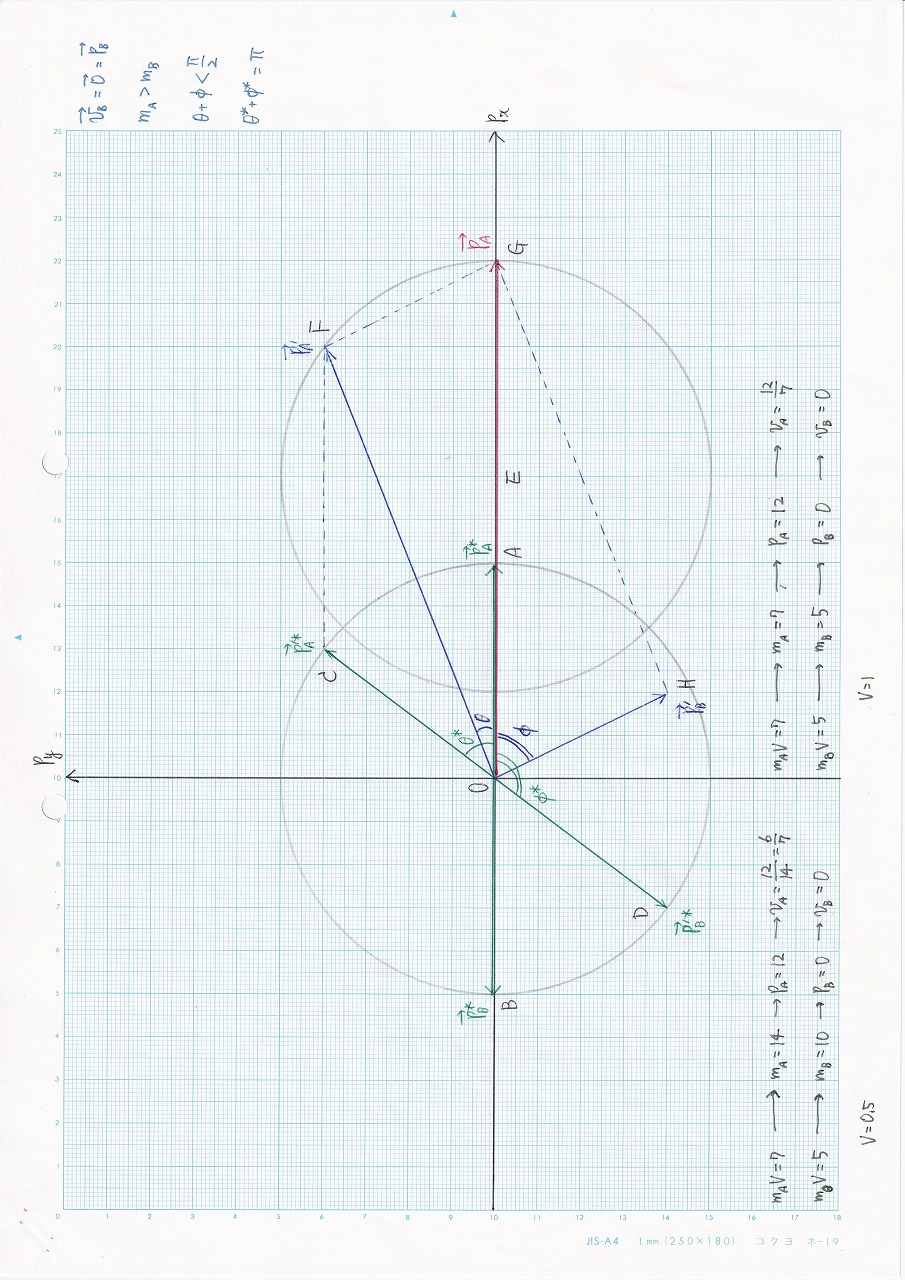  図3.17：vB= 0，mA>mB	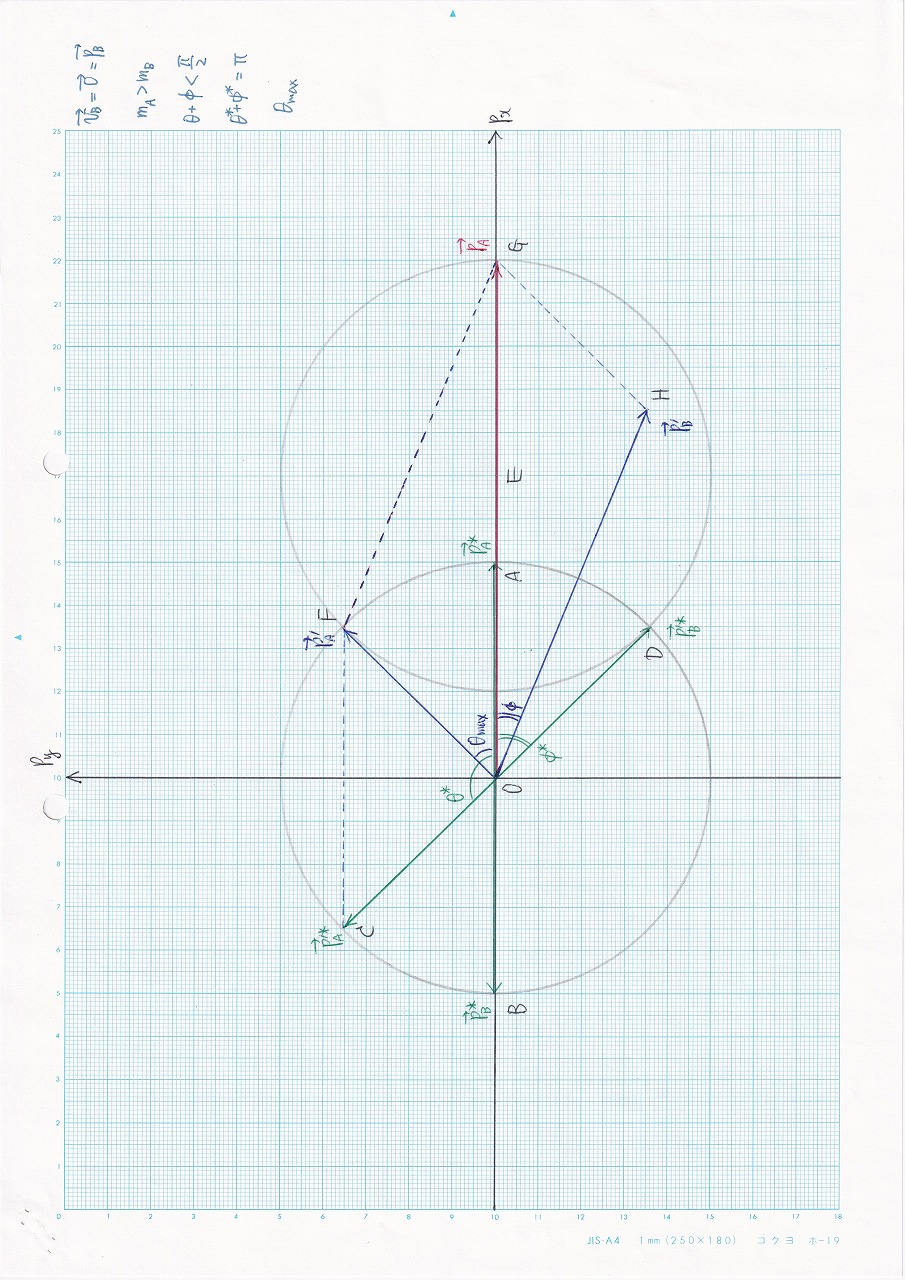図3.18：vB= 0，mA>mB

  ---

• 第5章

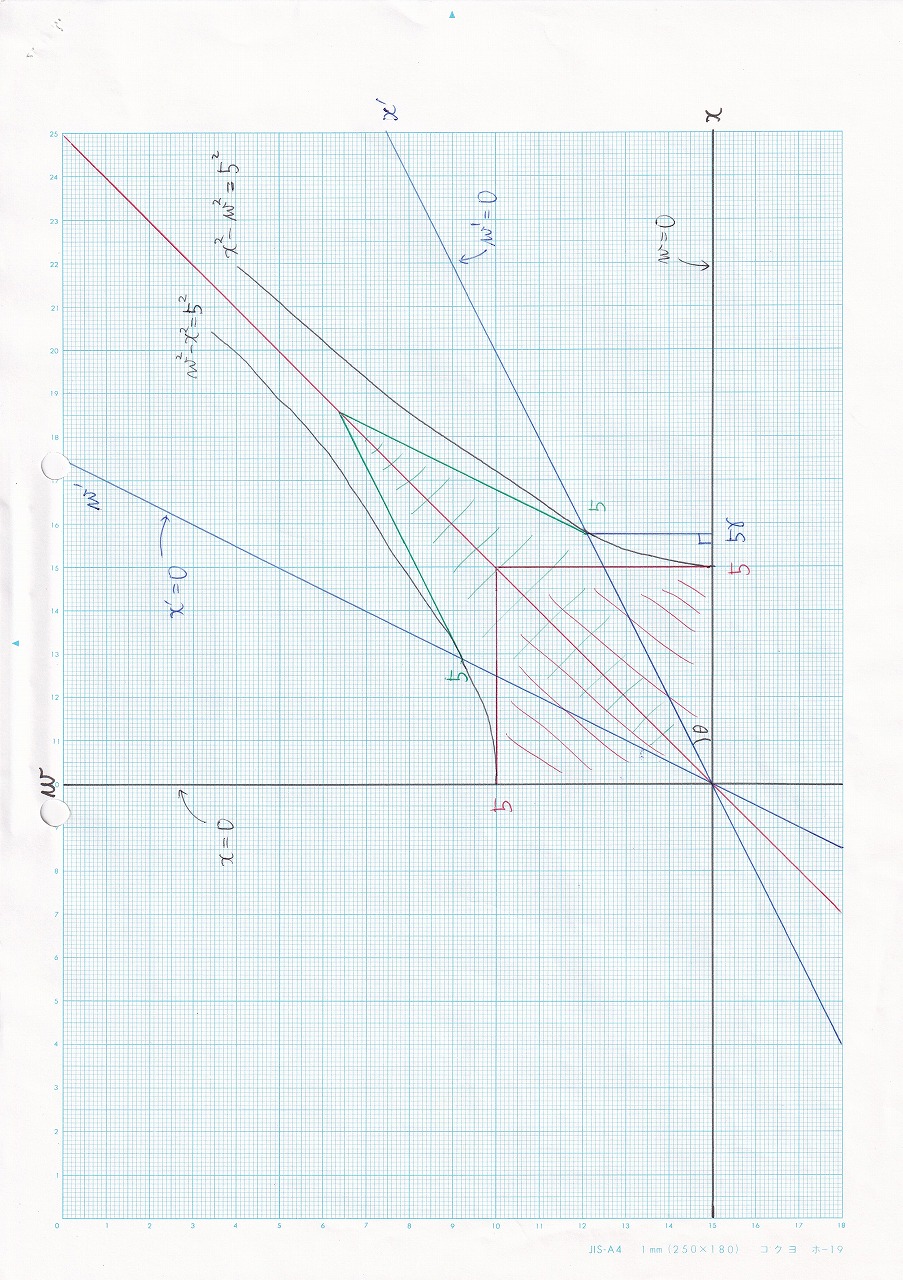  図5.1～5.4	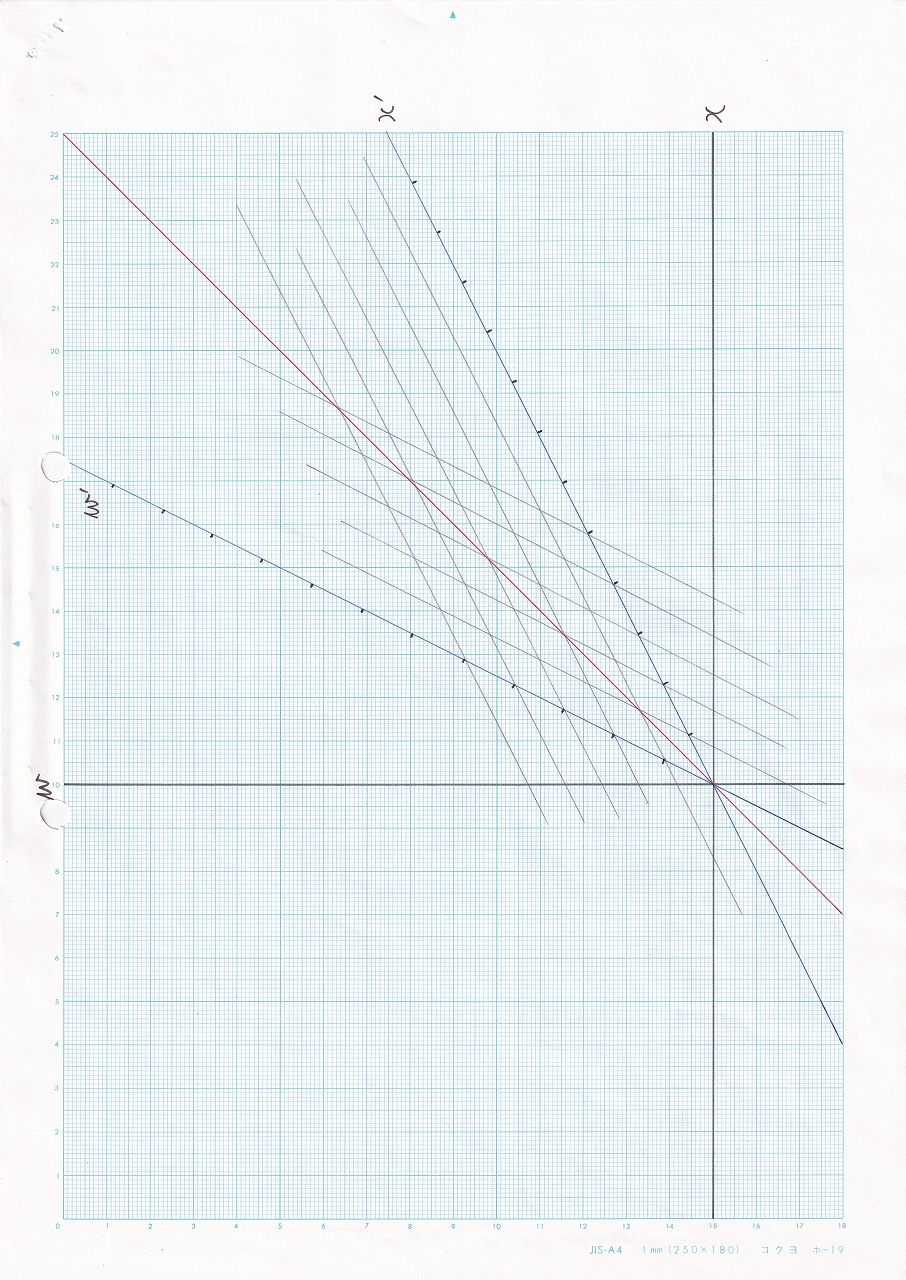なし
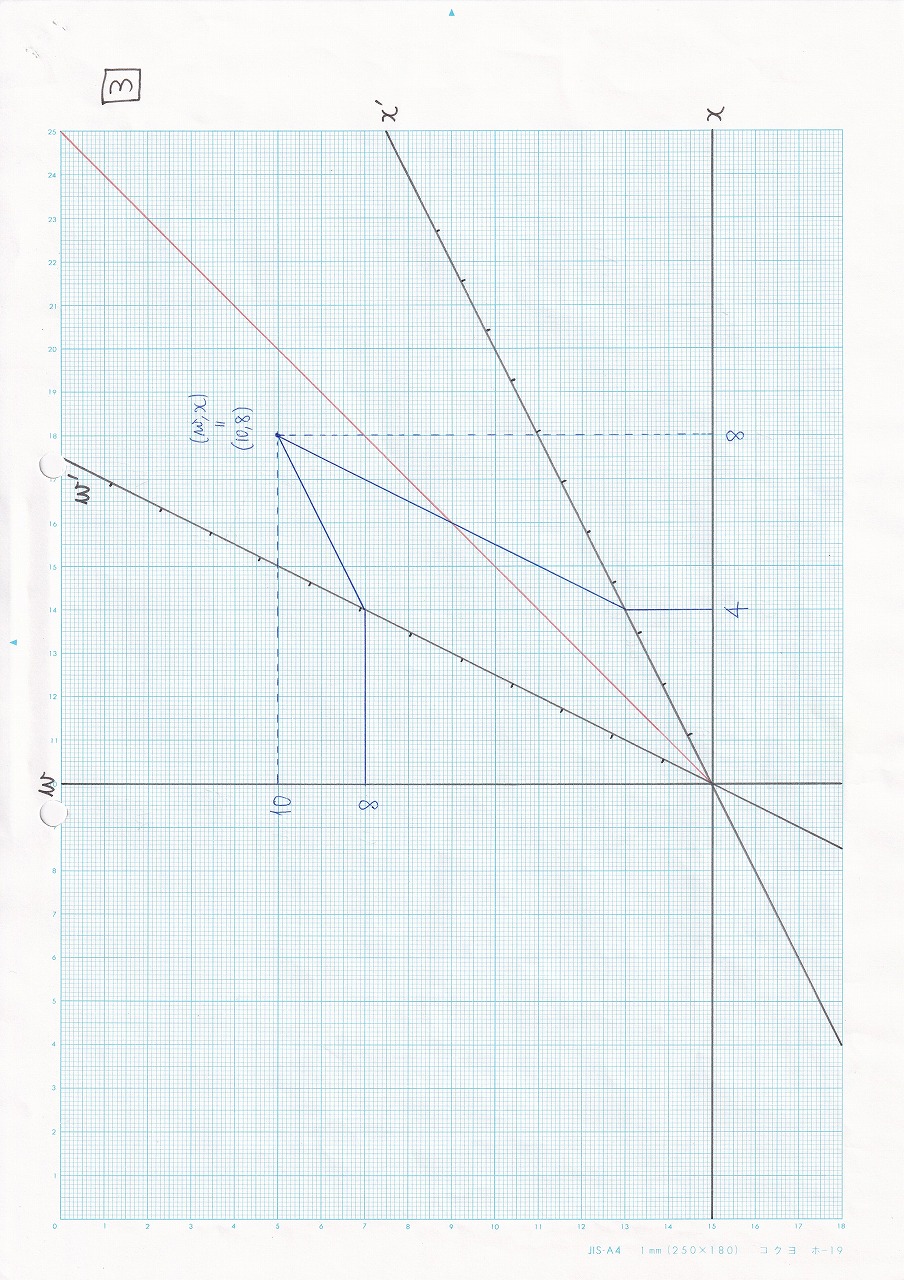  図5.6	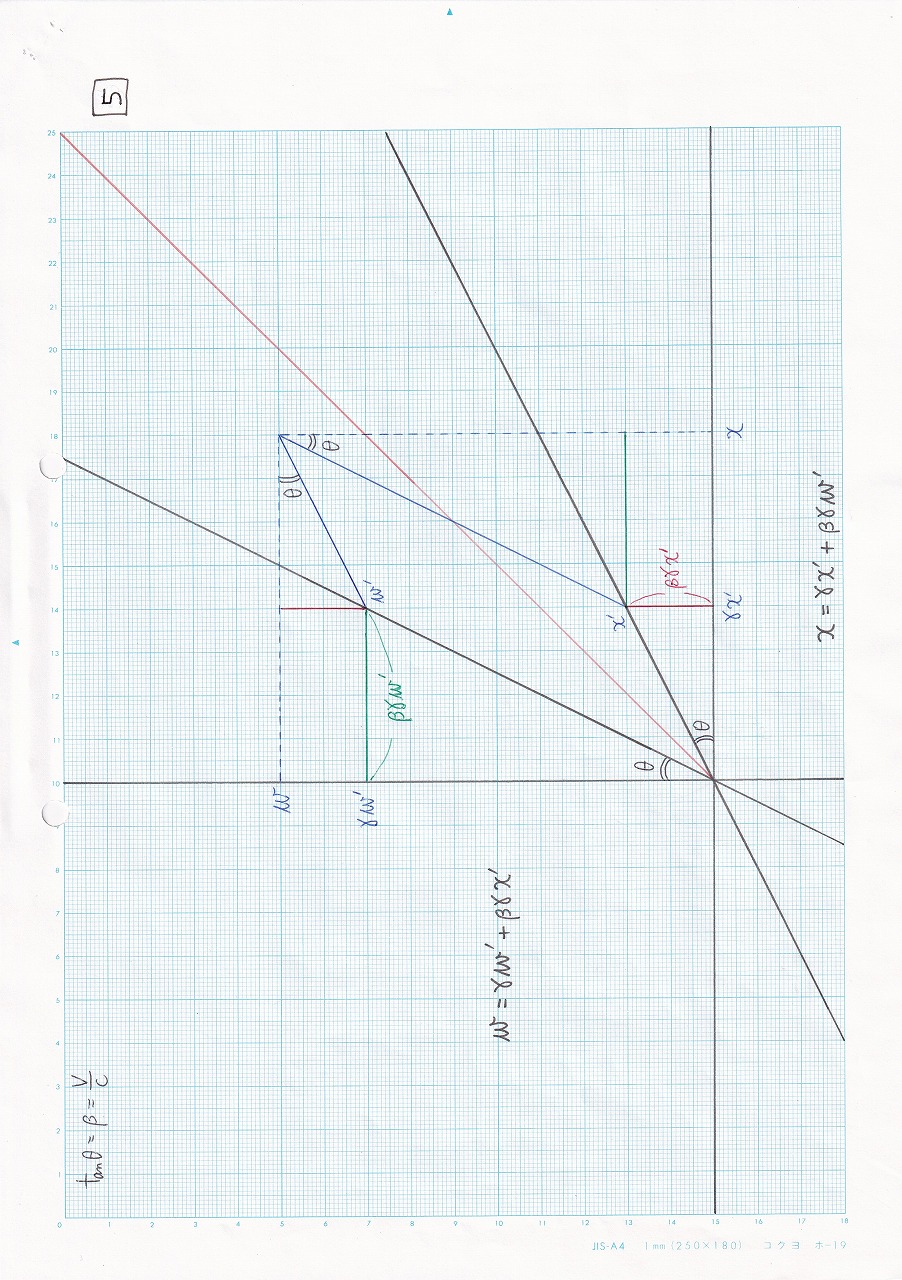図5.7
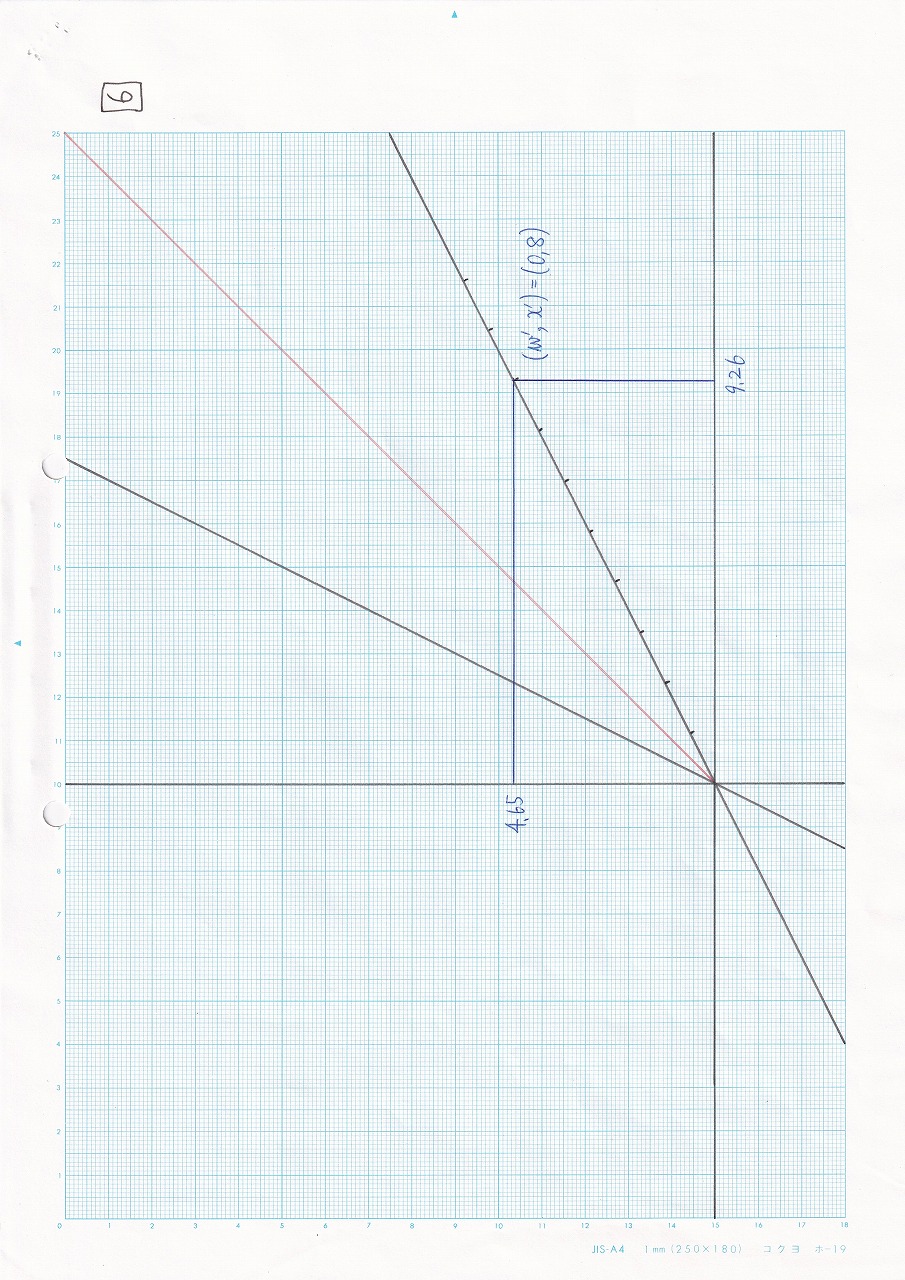  図5.8	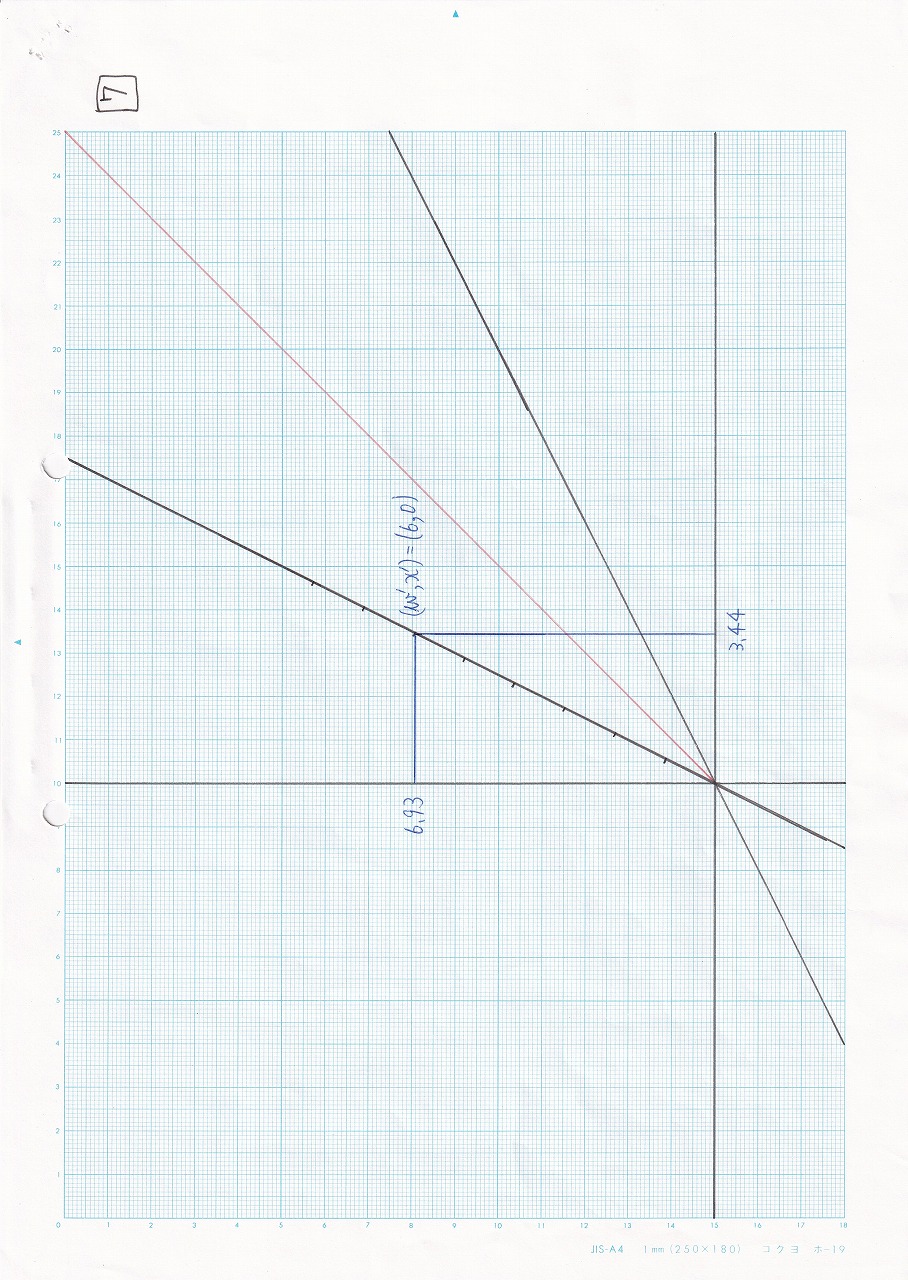図5.9
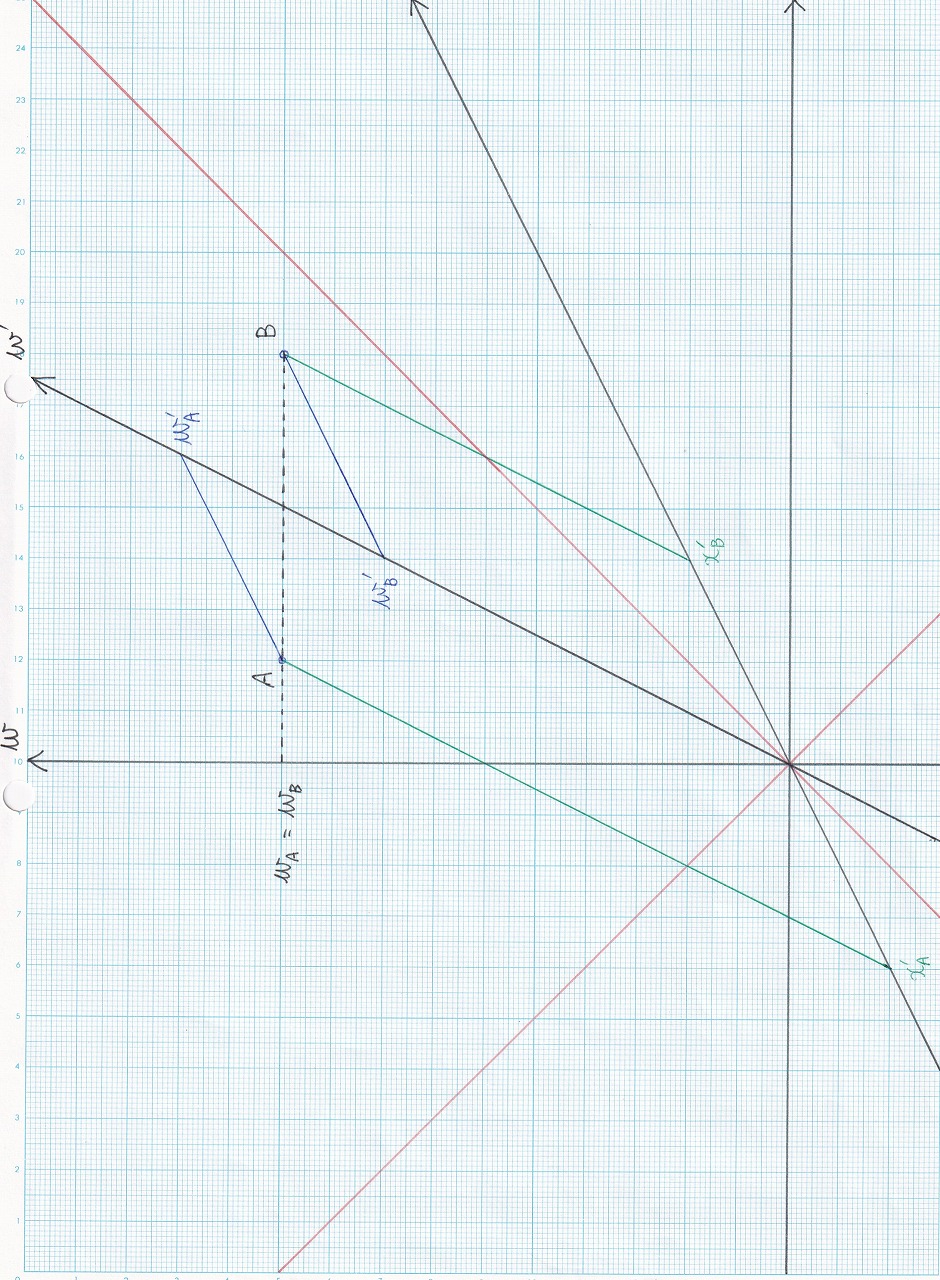  図5.10	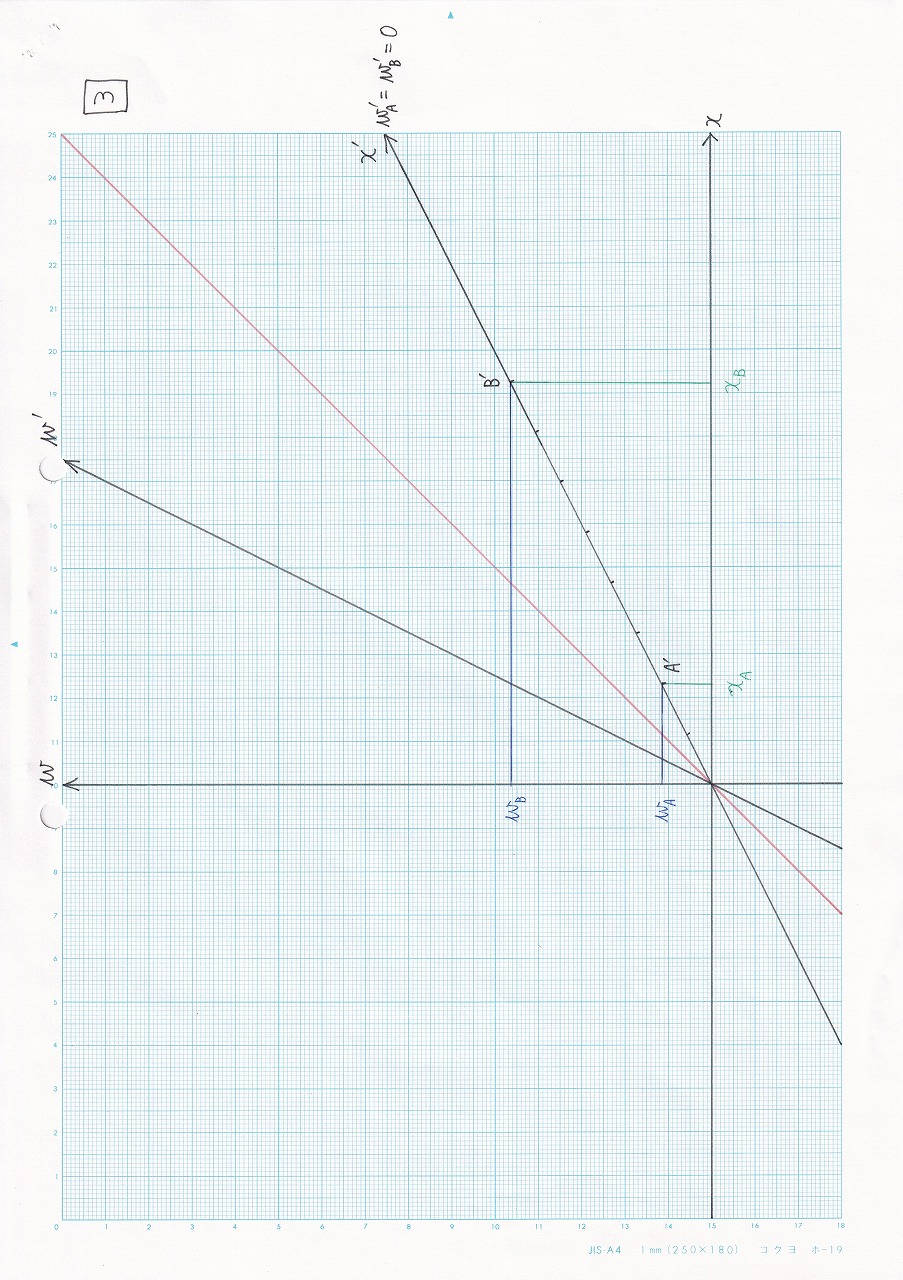図5.11
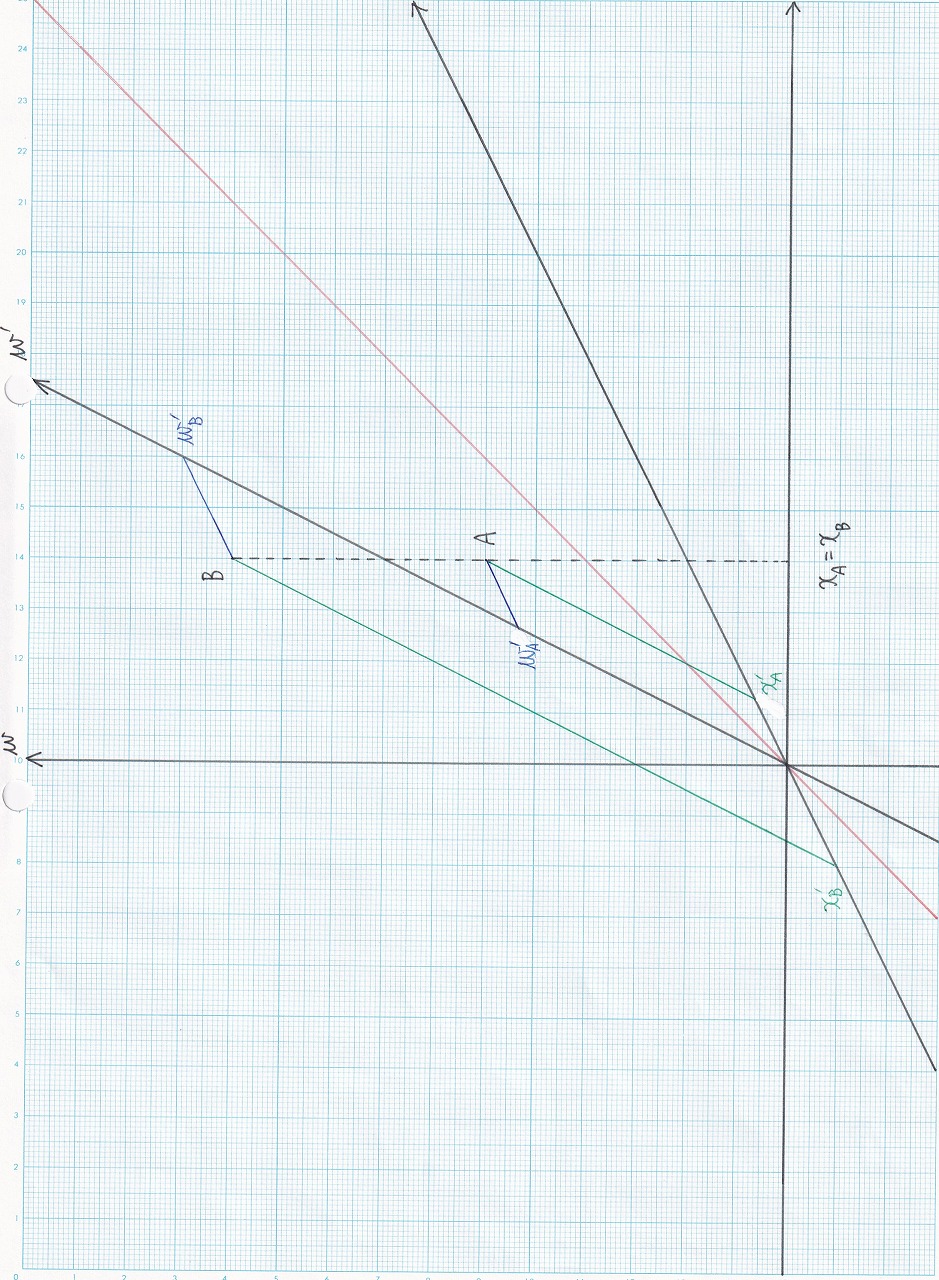  図5.12	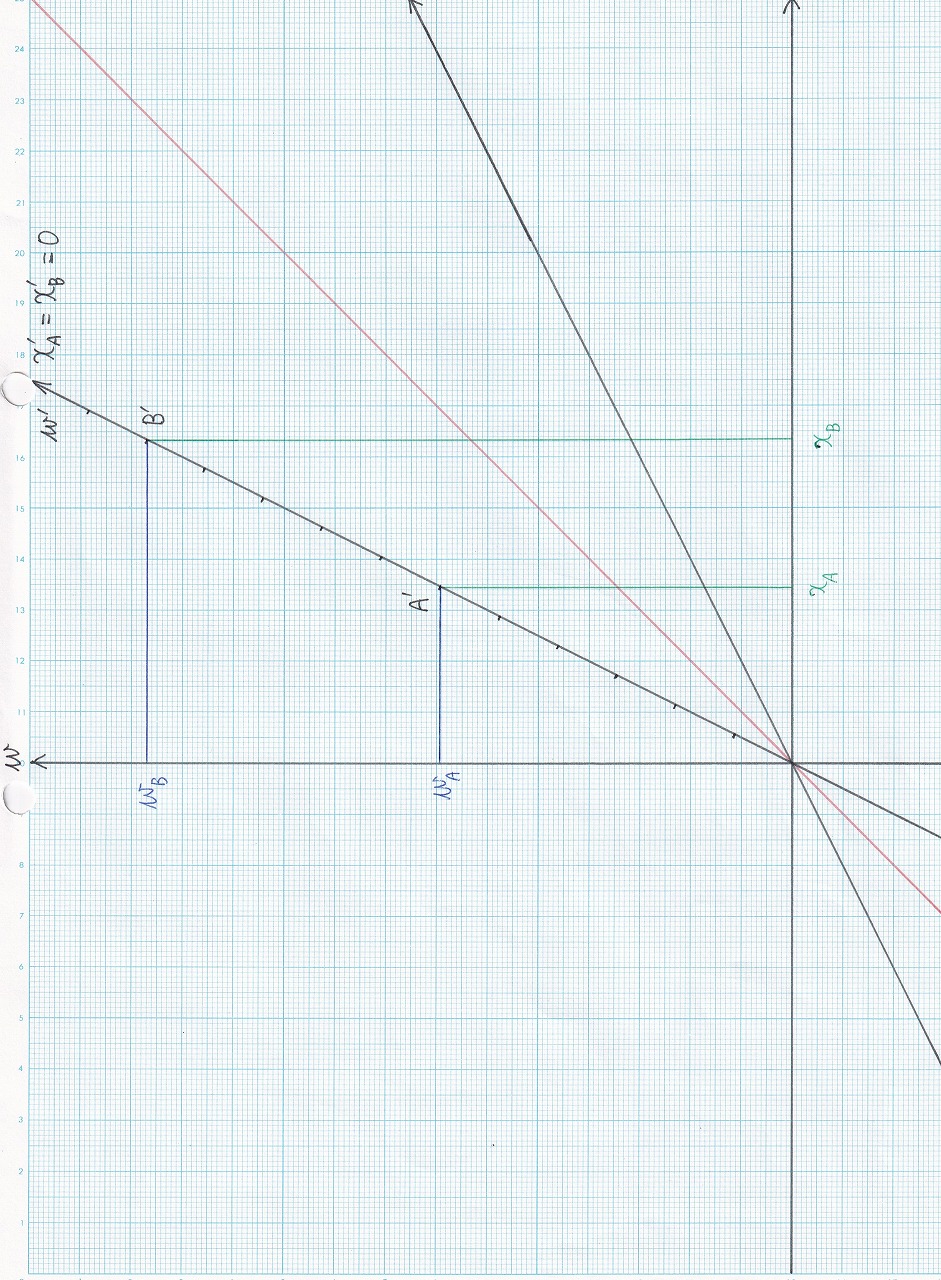図5.13
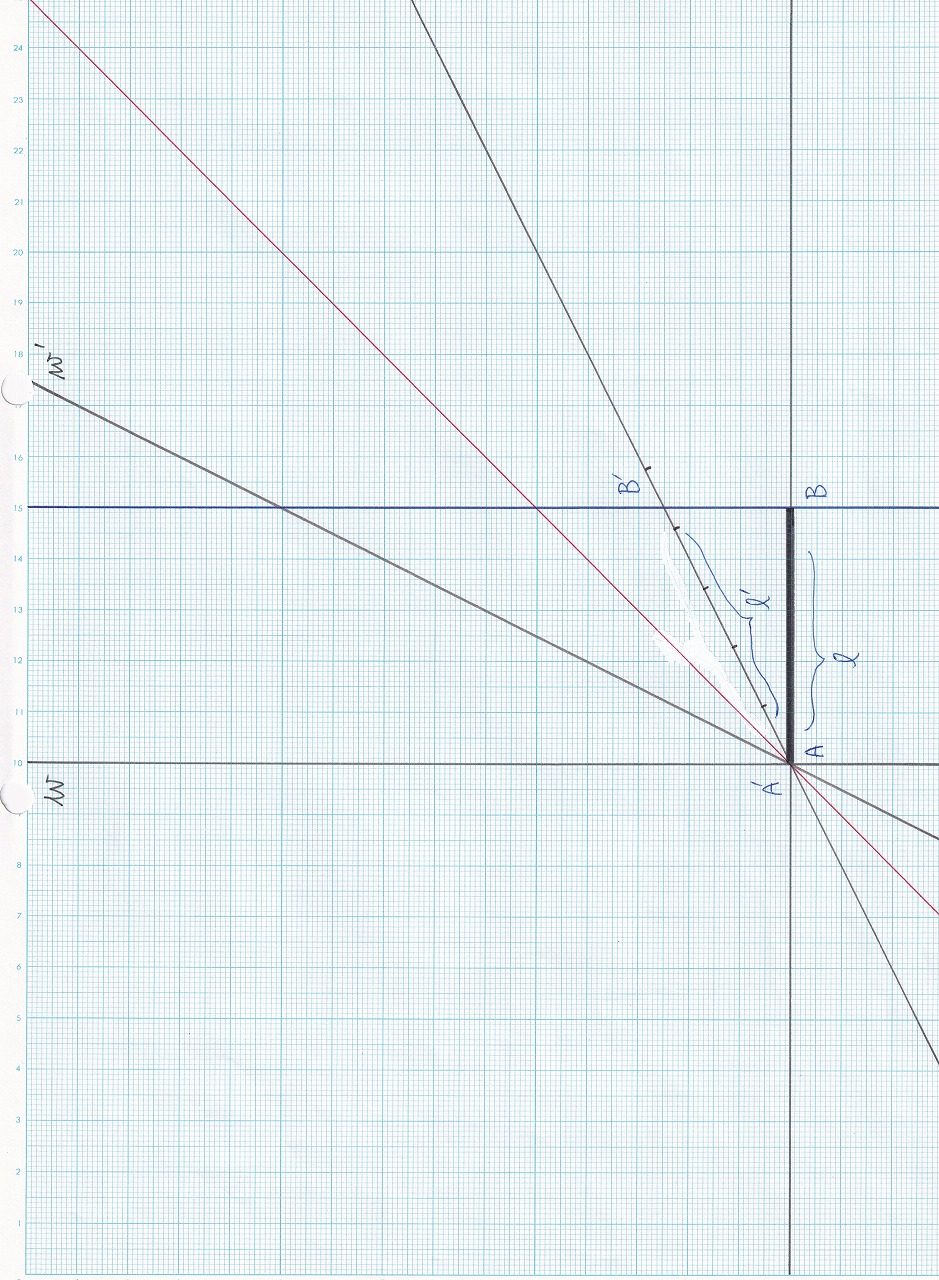  図5.14	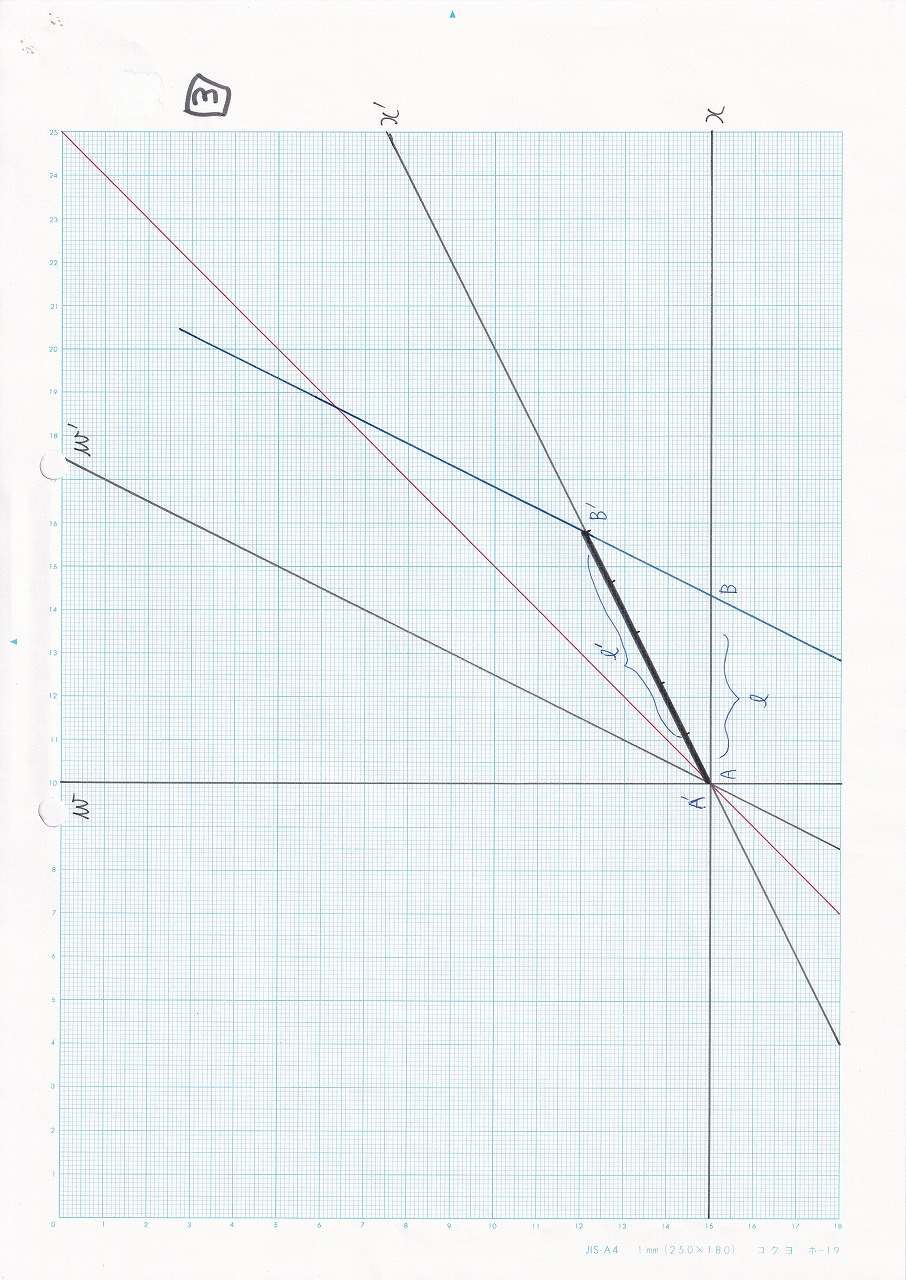図5.15
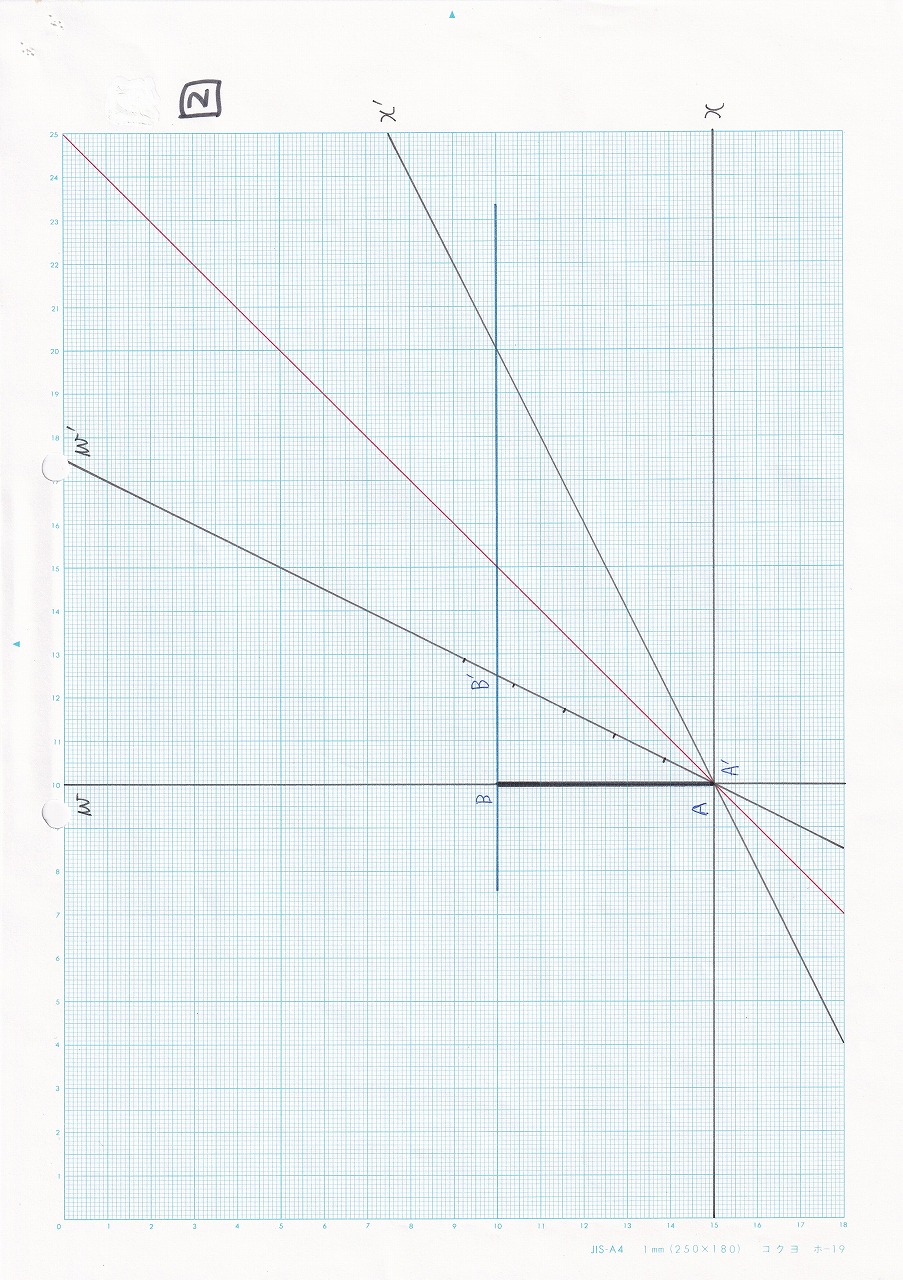  図5.16	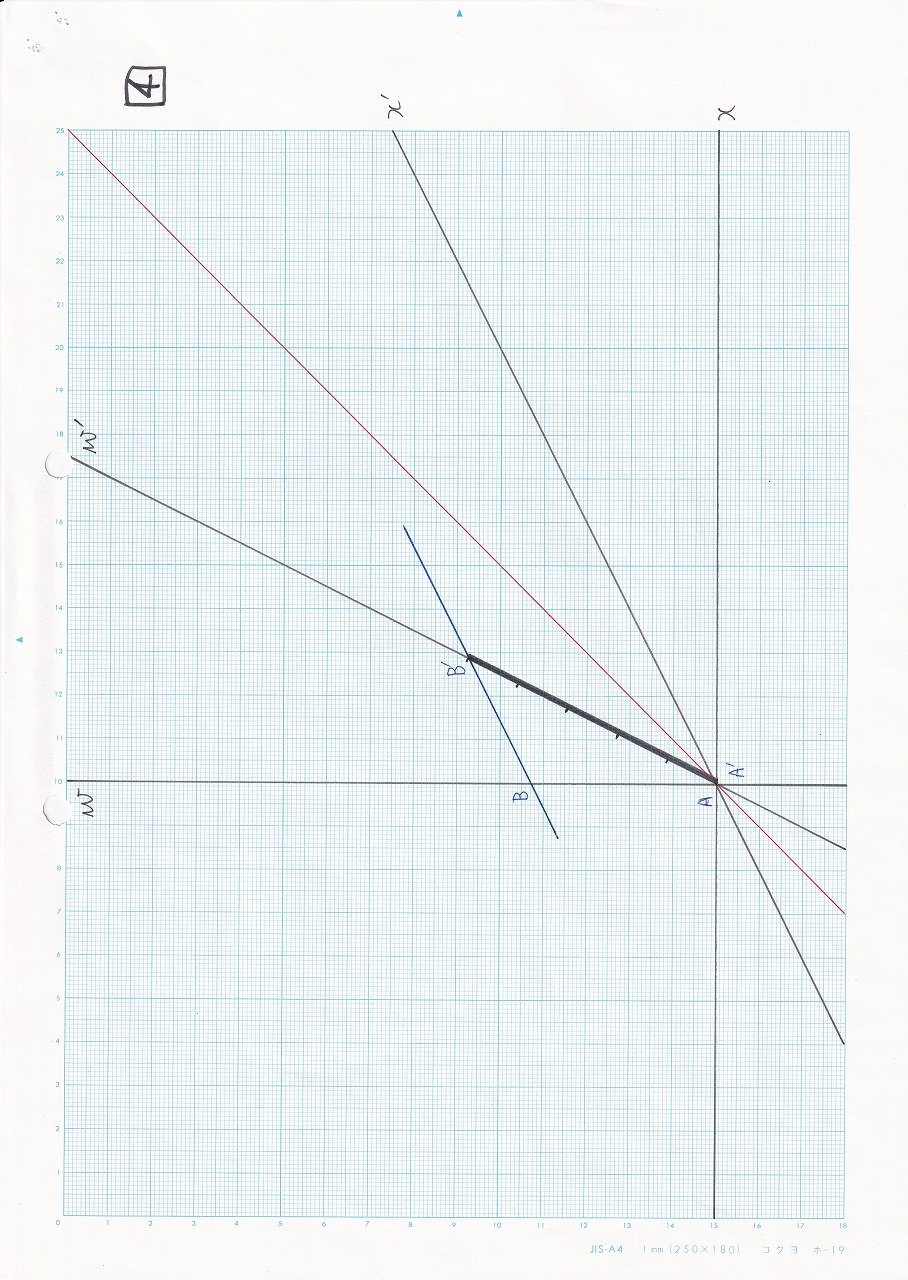図5.17
  図5.18	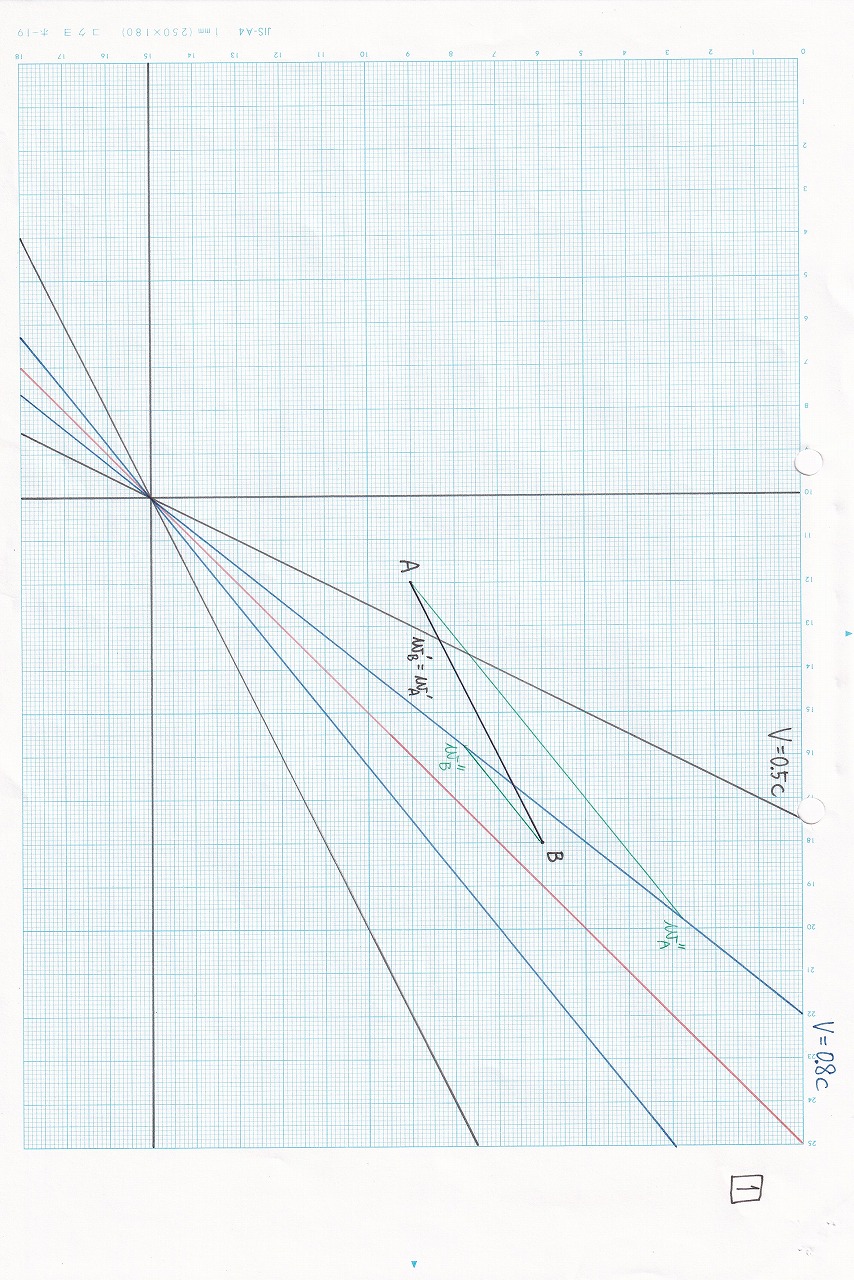図5.20
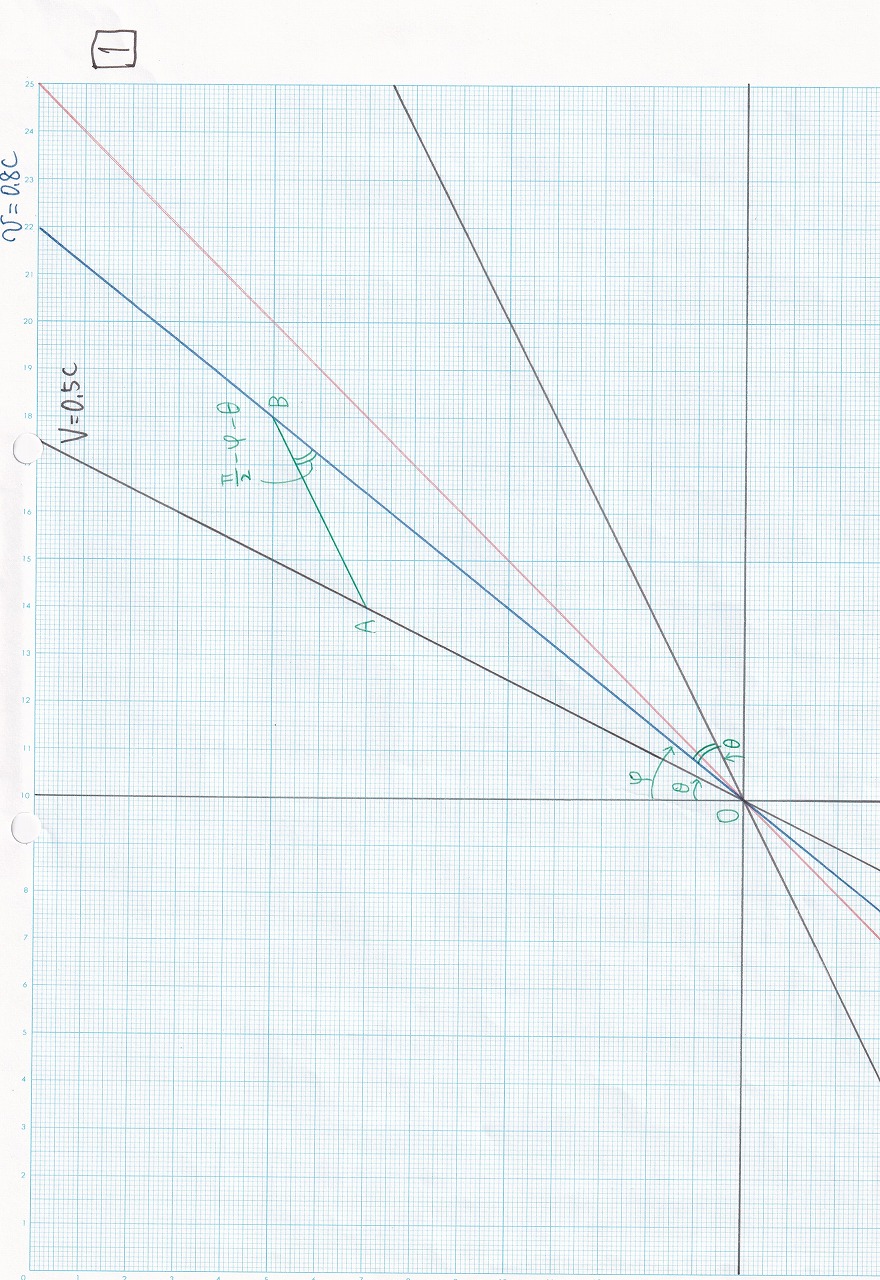  図5.21	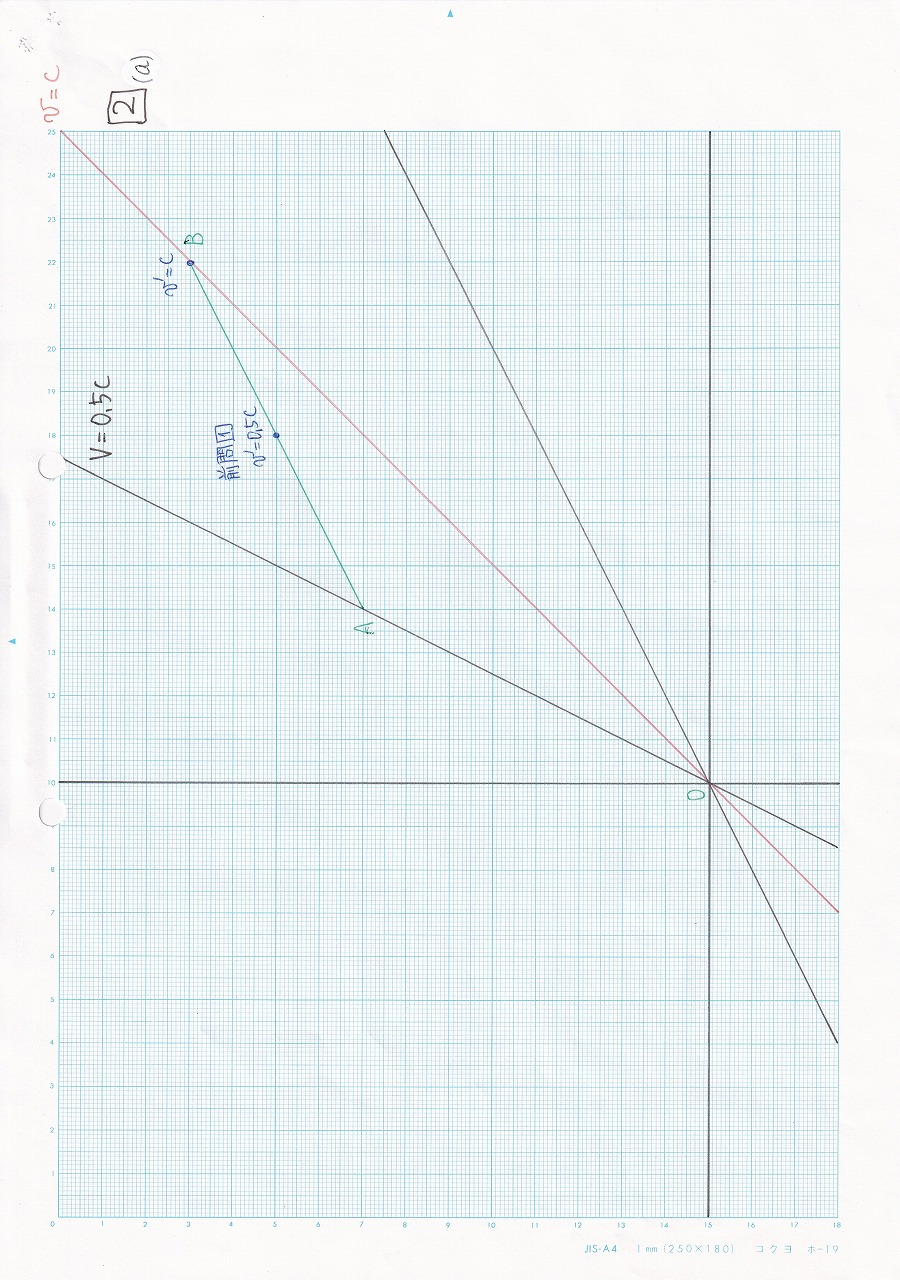図5.22
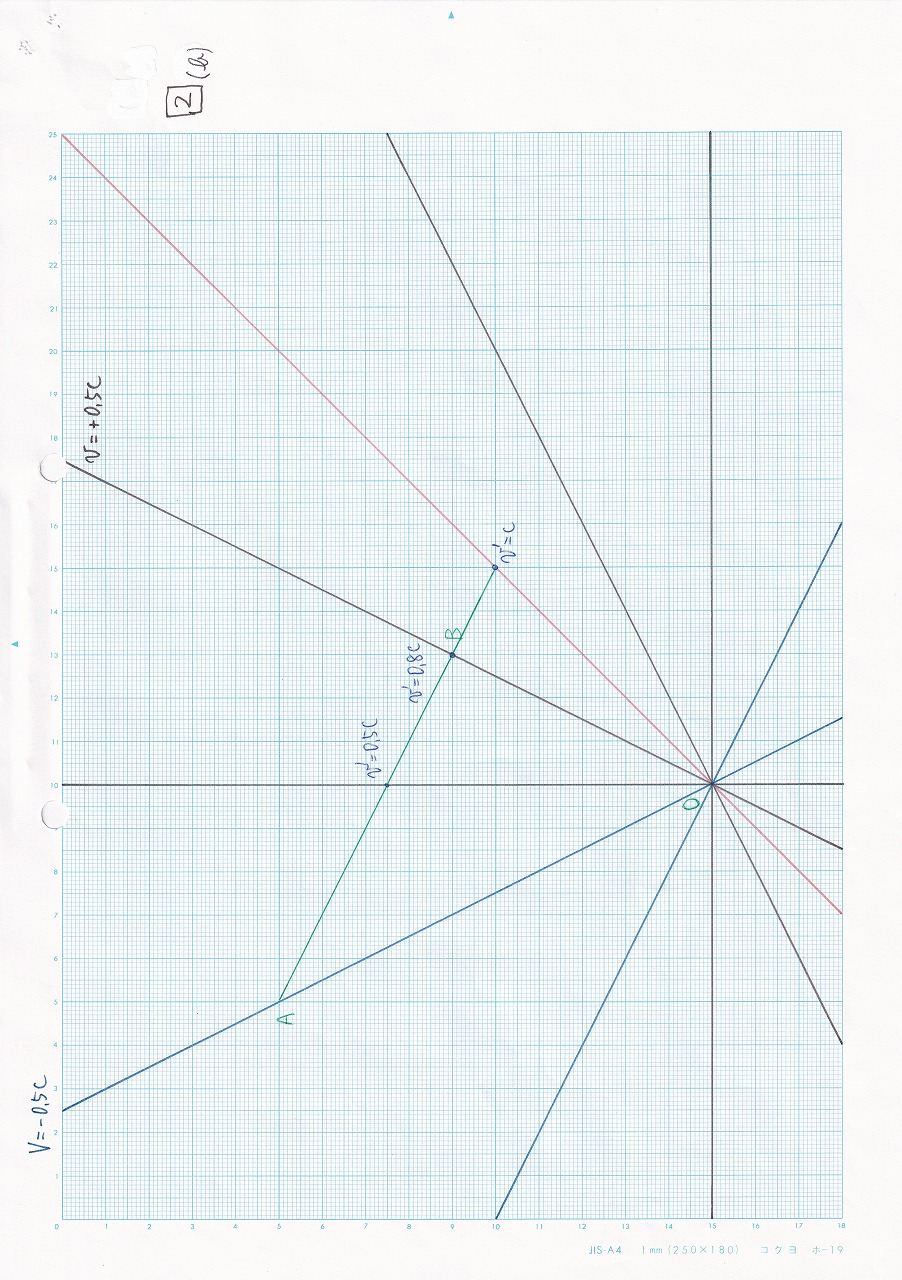  図5.23	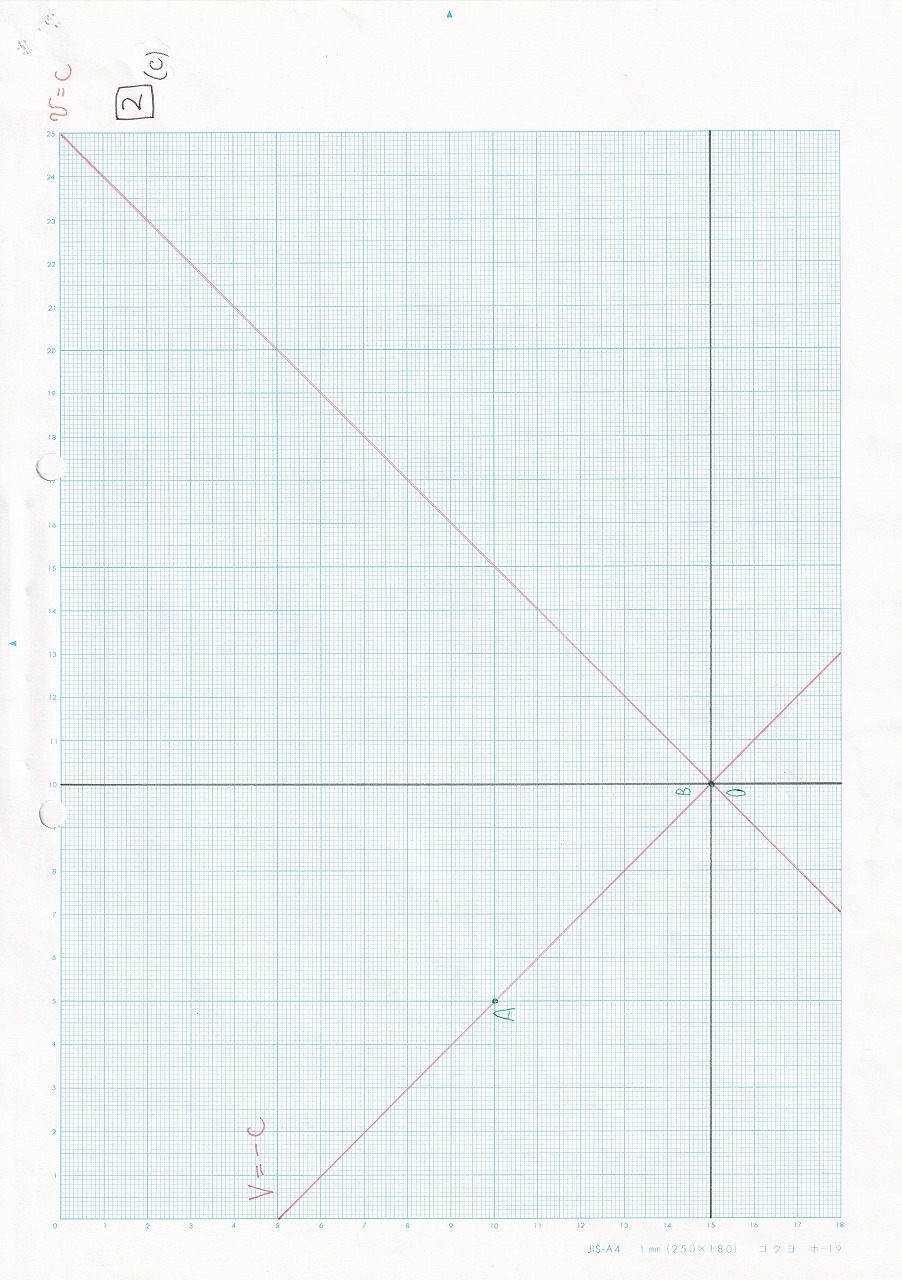なし
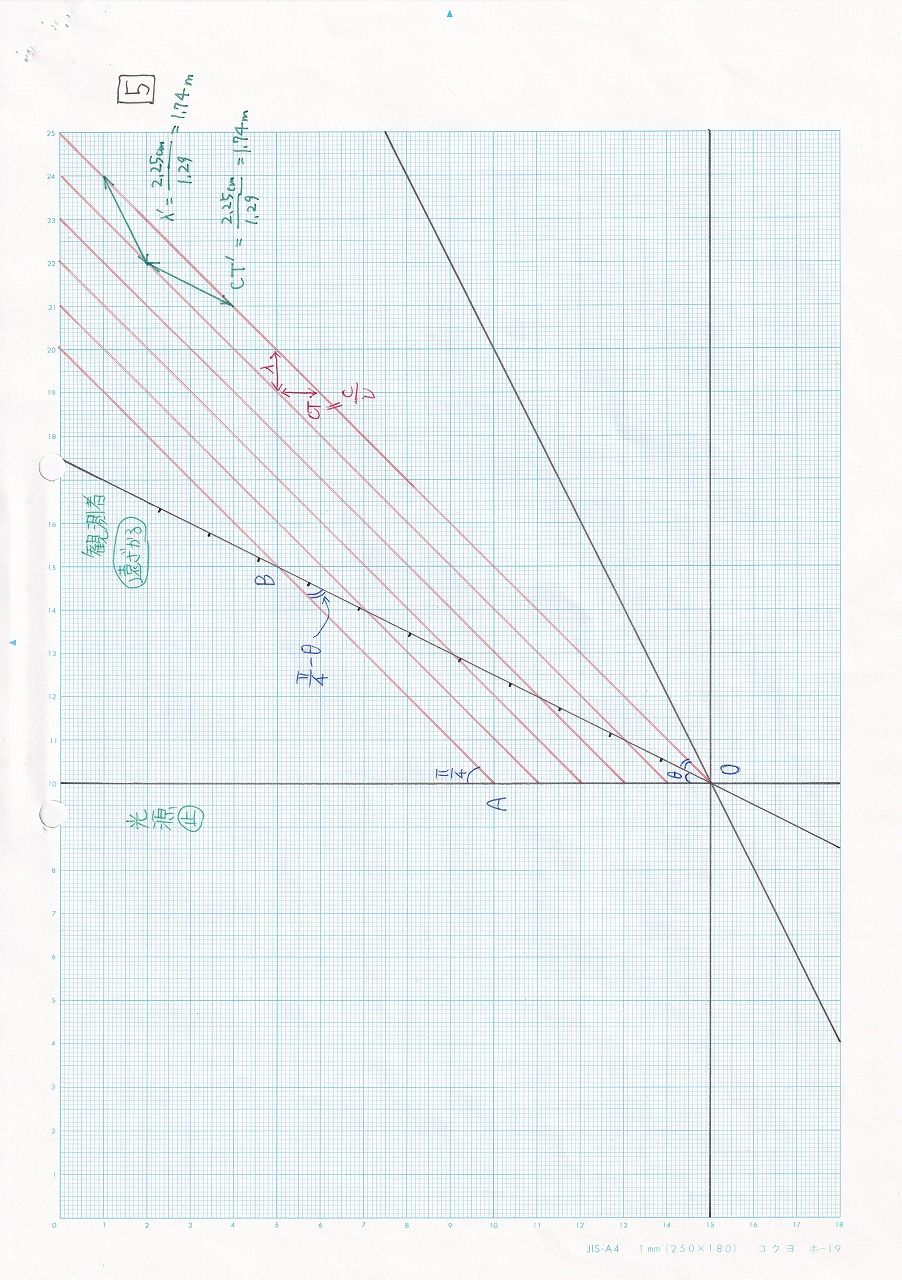  図5.26	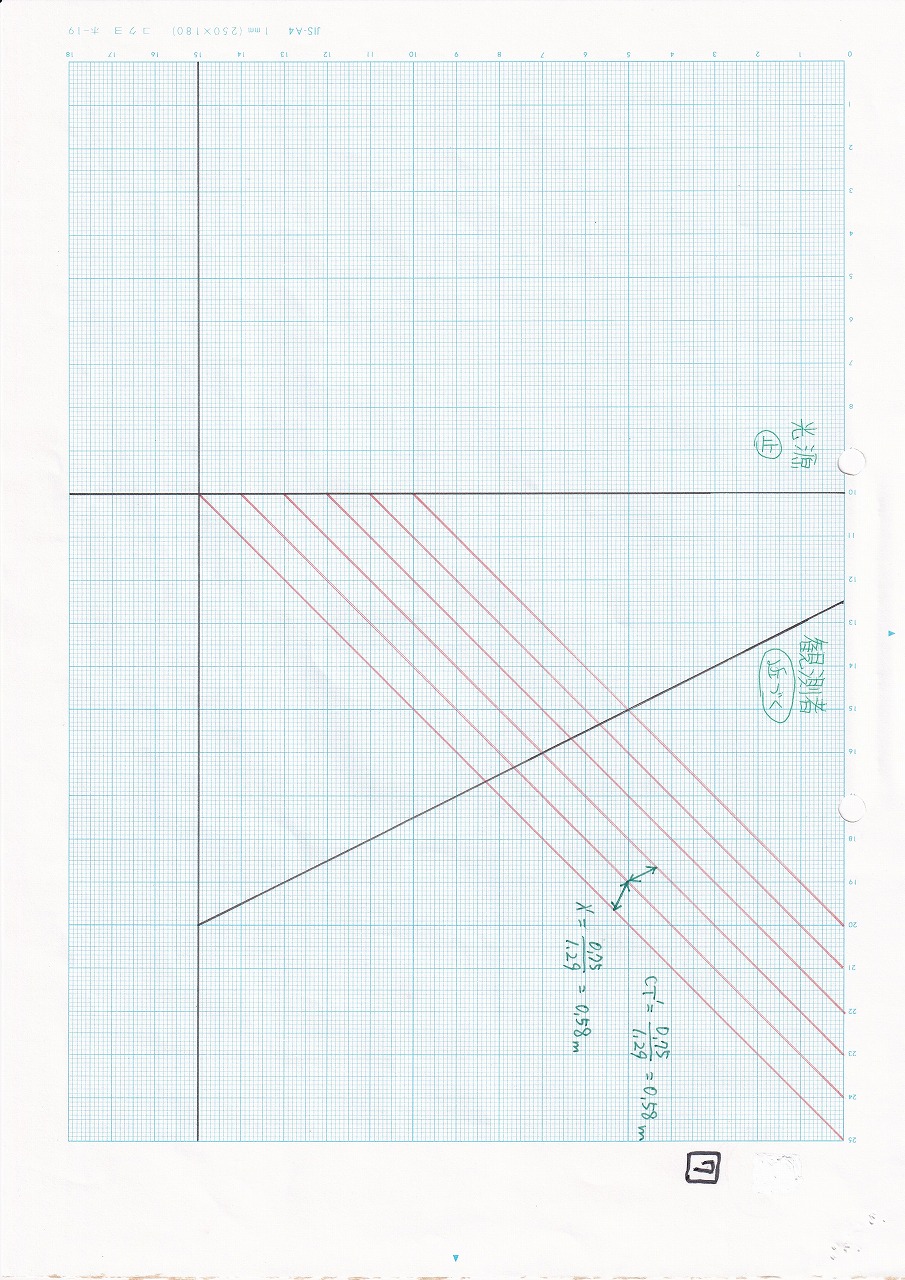図5.27
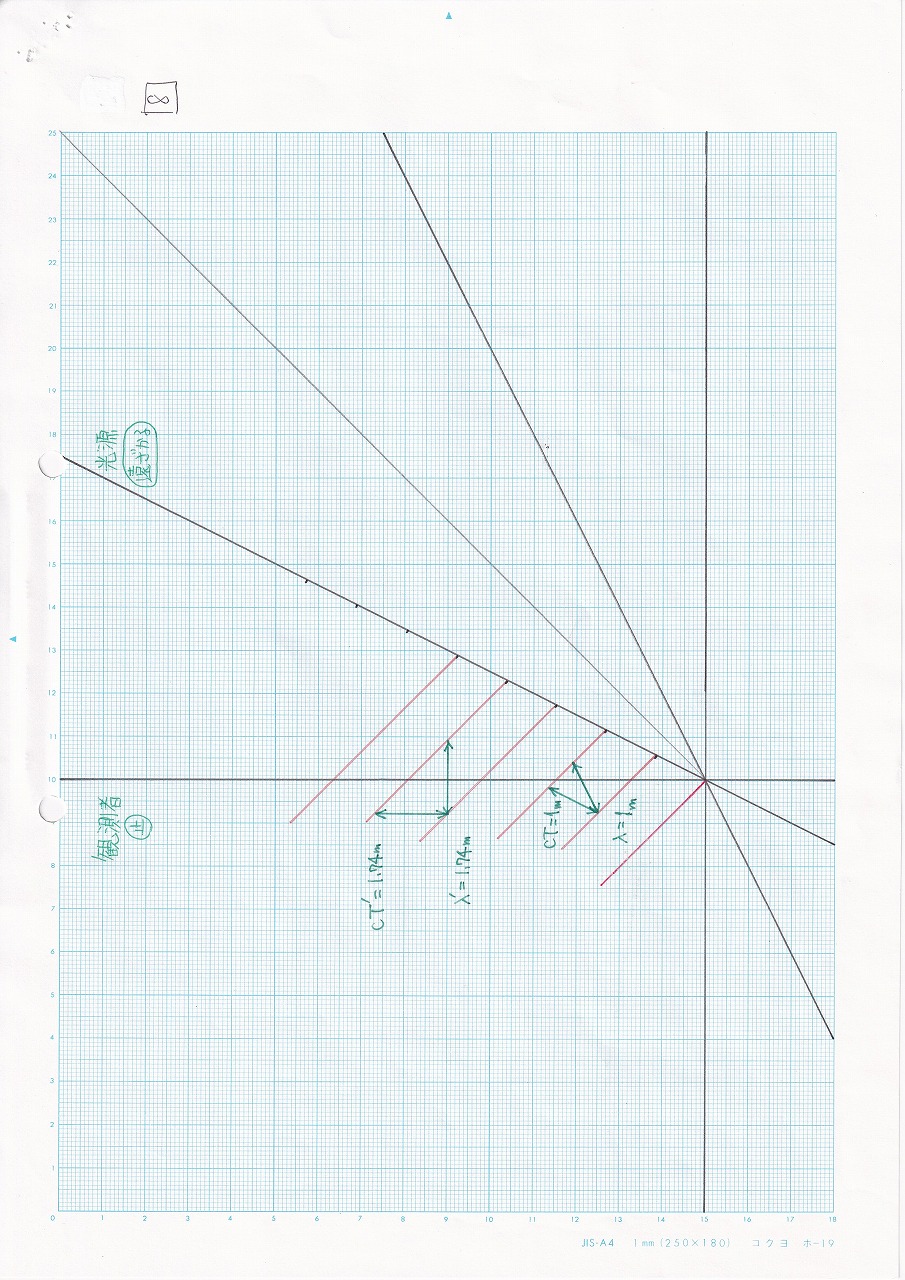  図5.28	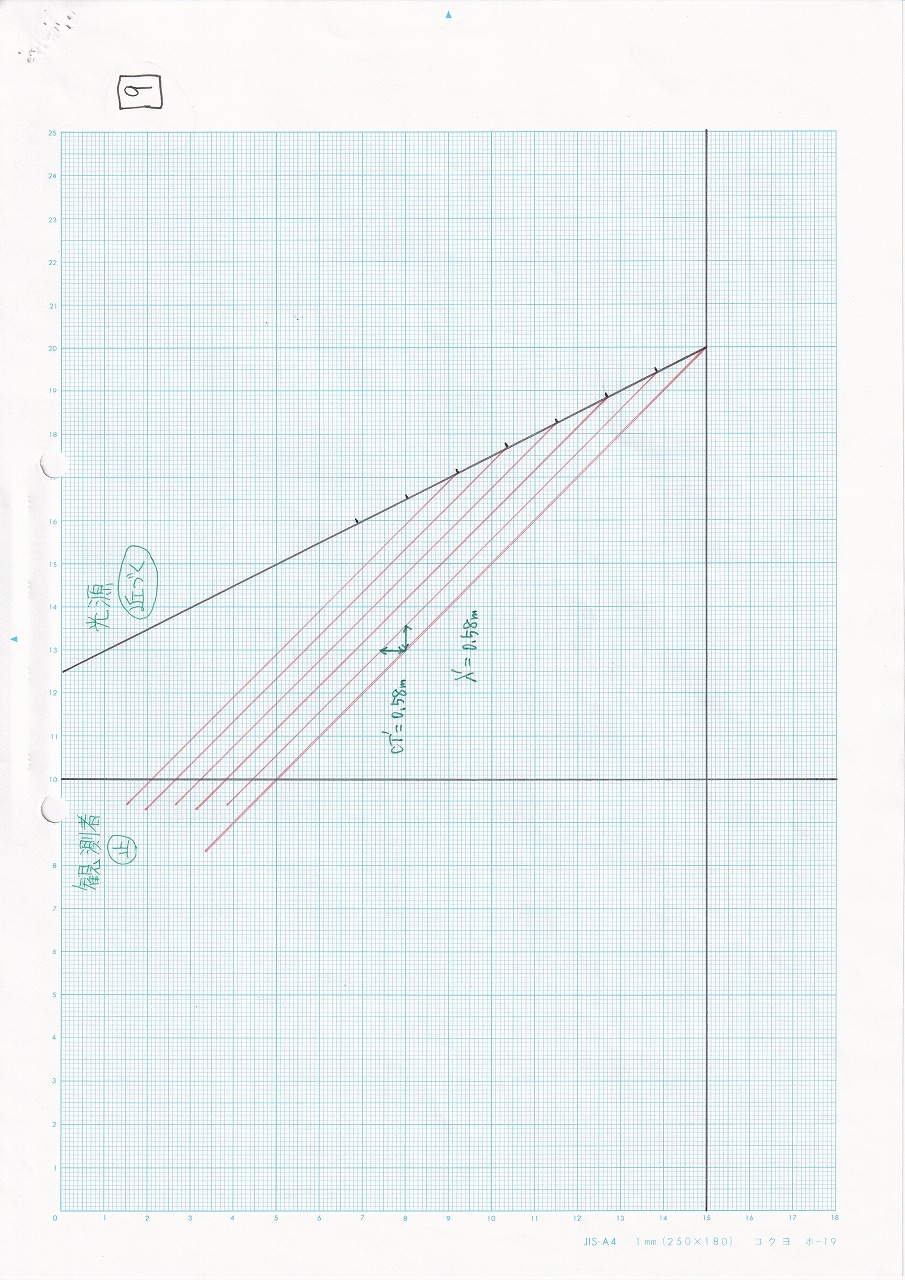図5.29

  ---

• 第6章

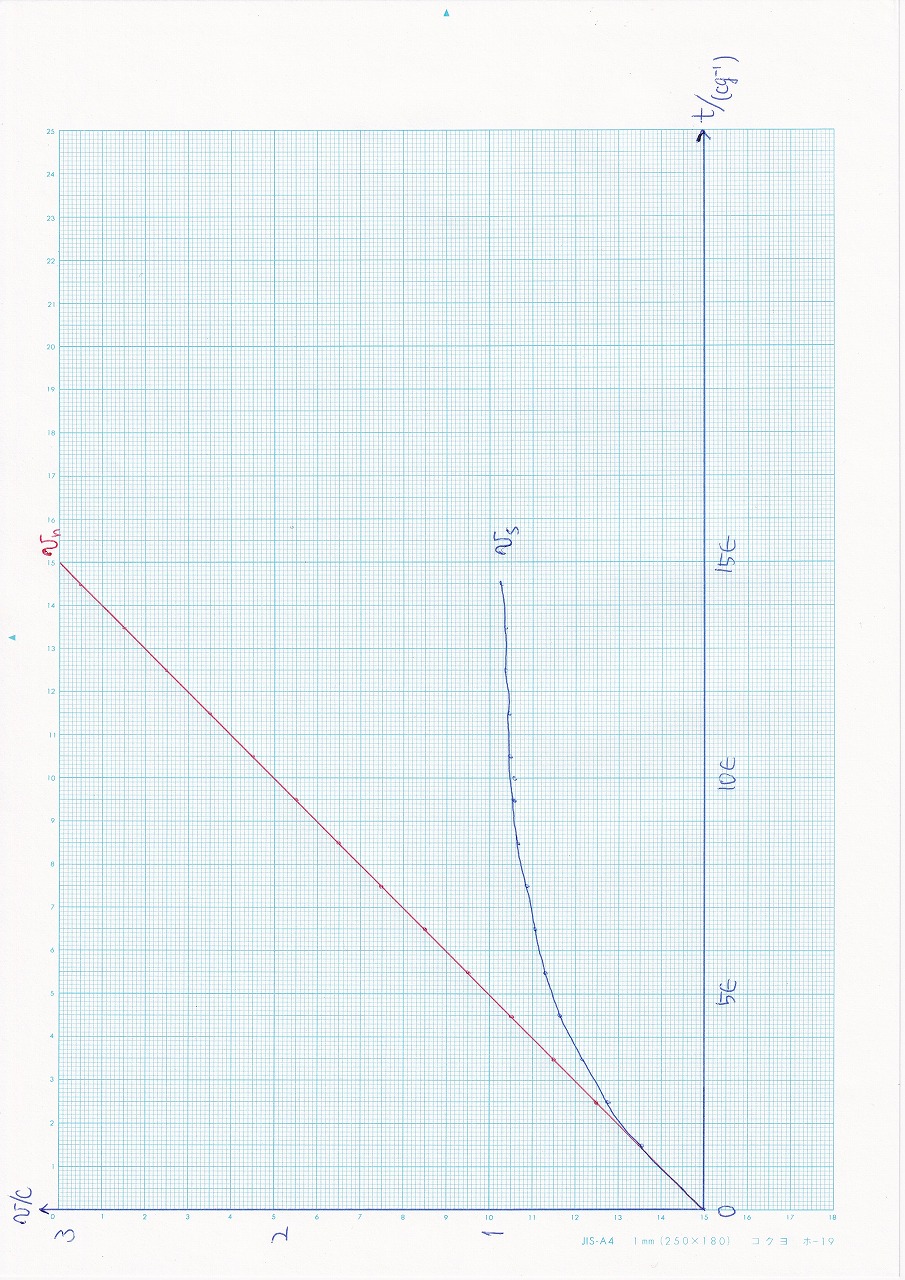  図6.1	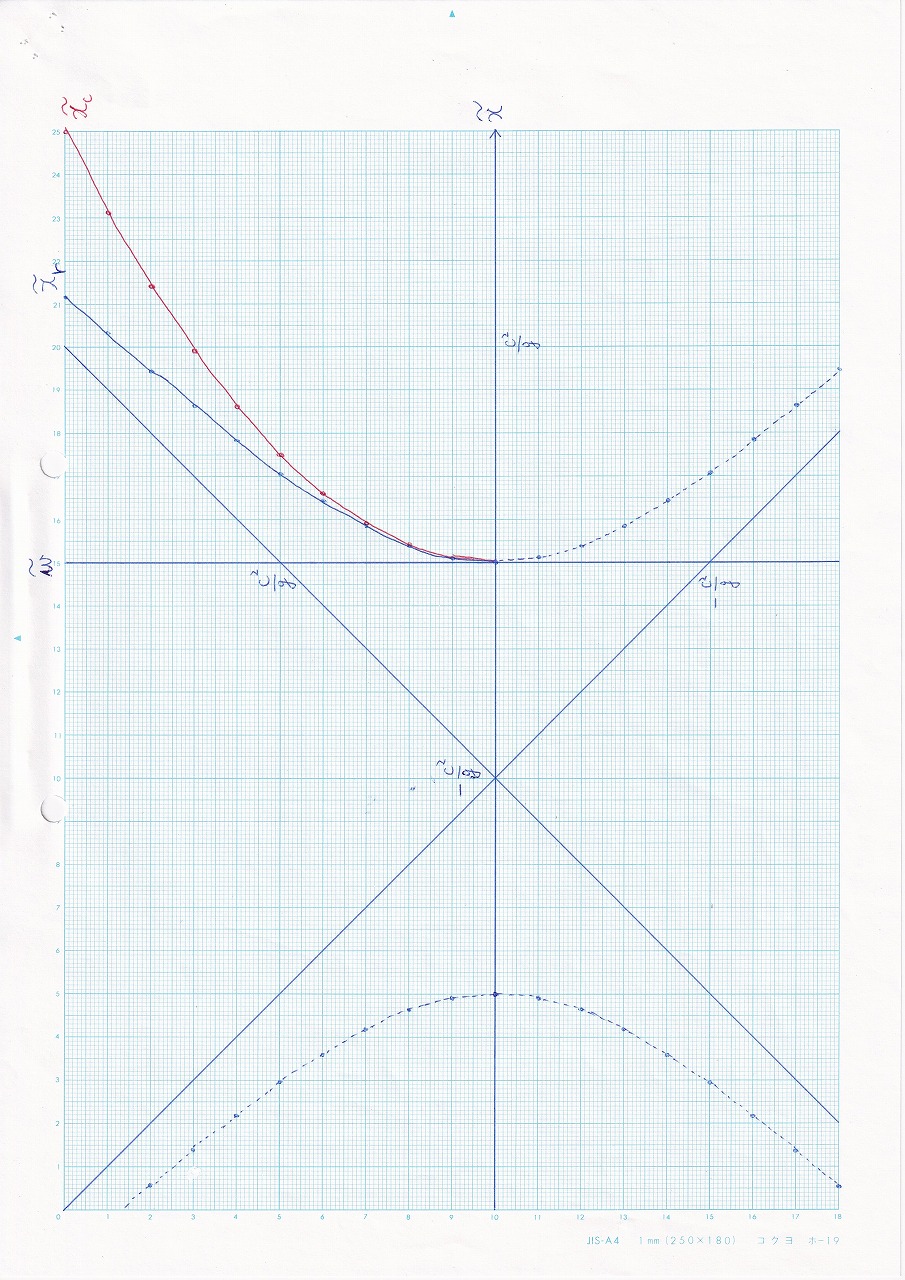図6.2
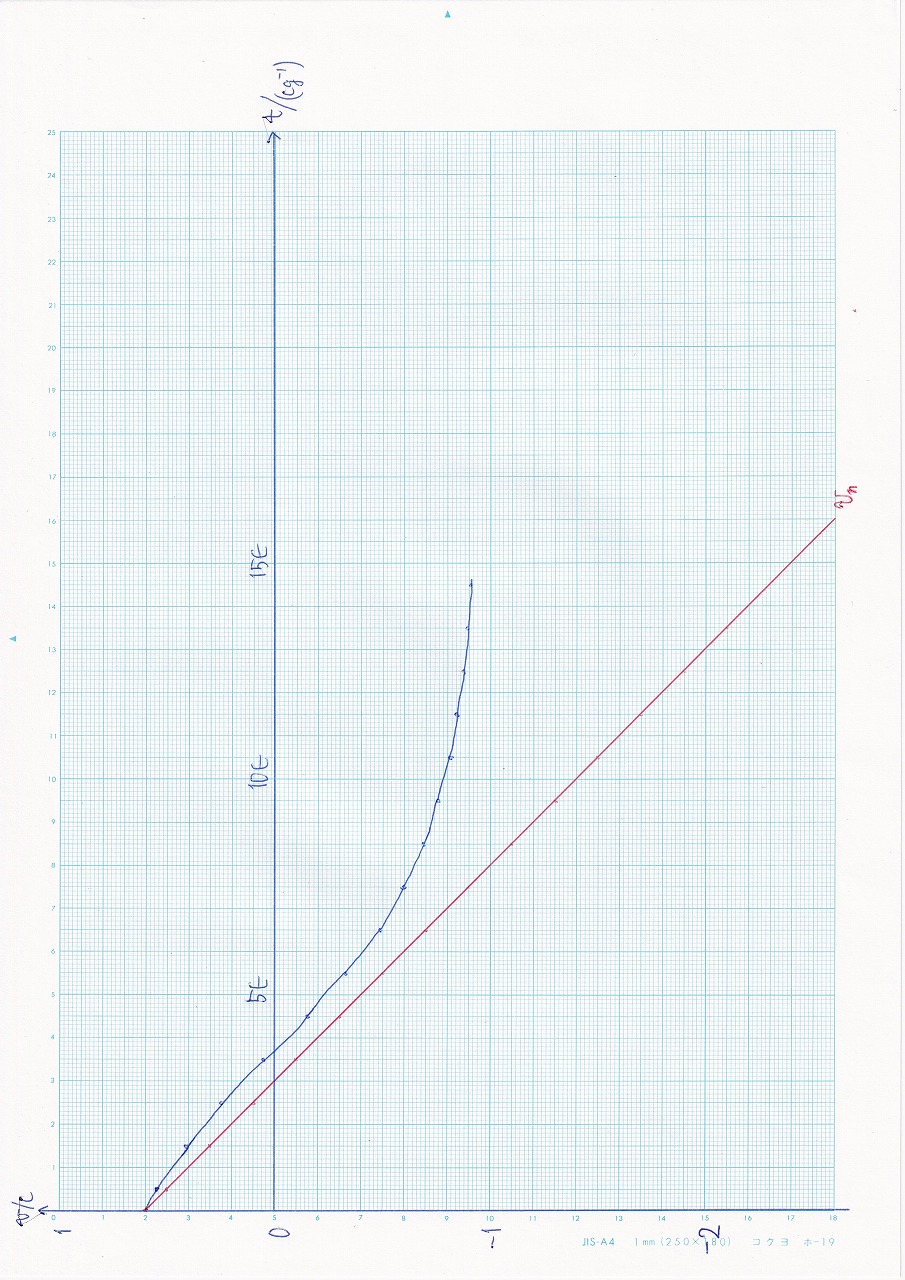  図6.3	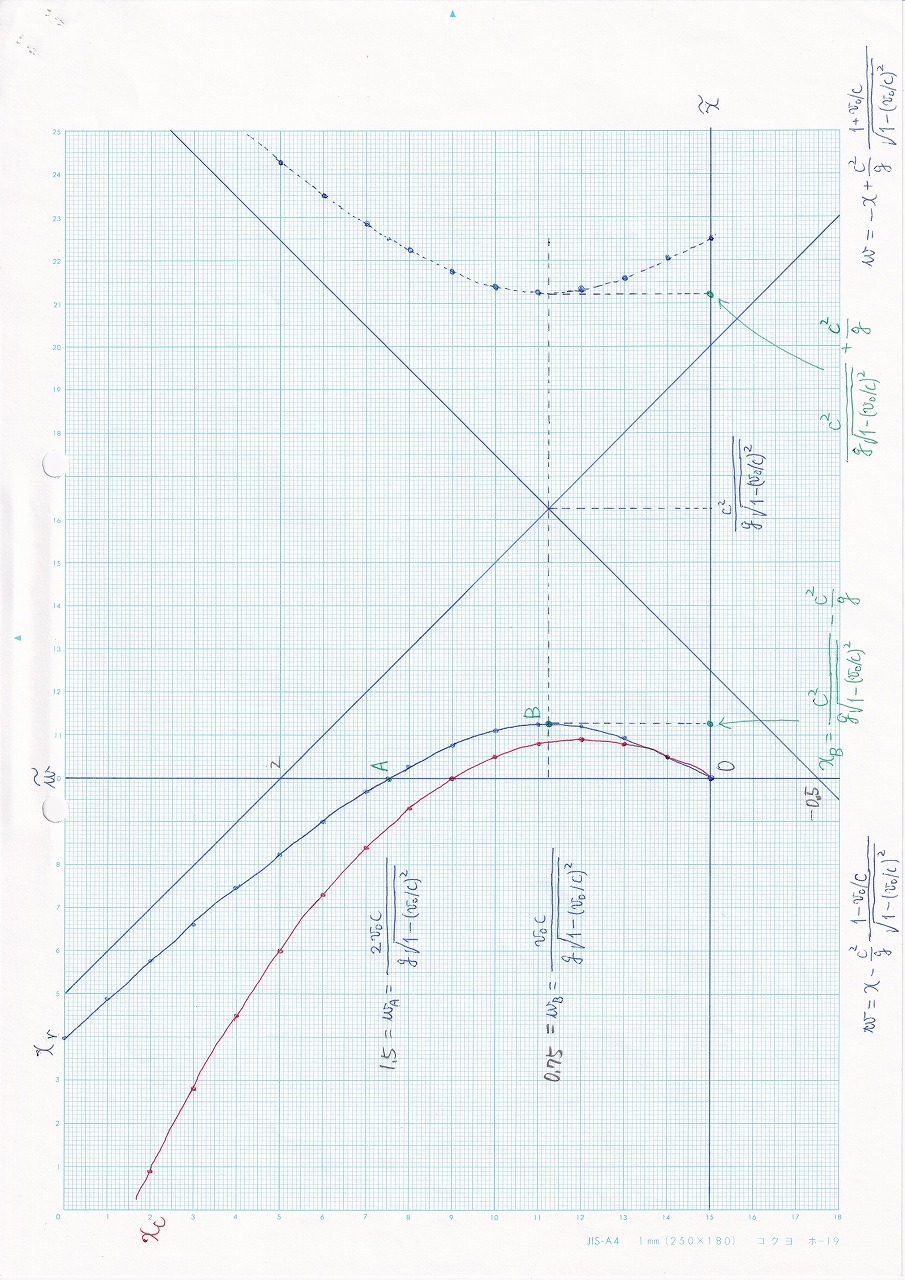図6.4

  ---

• 第7章

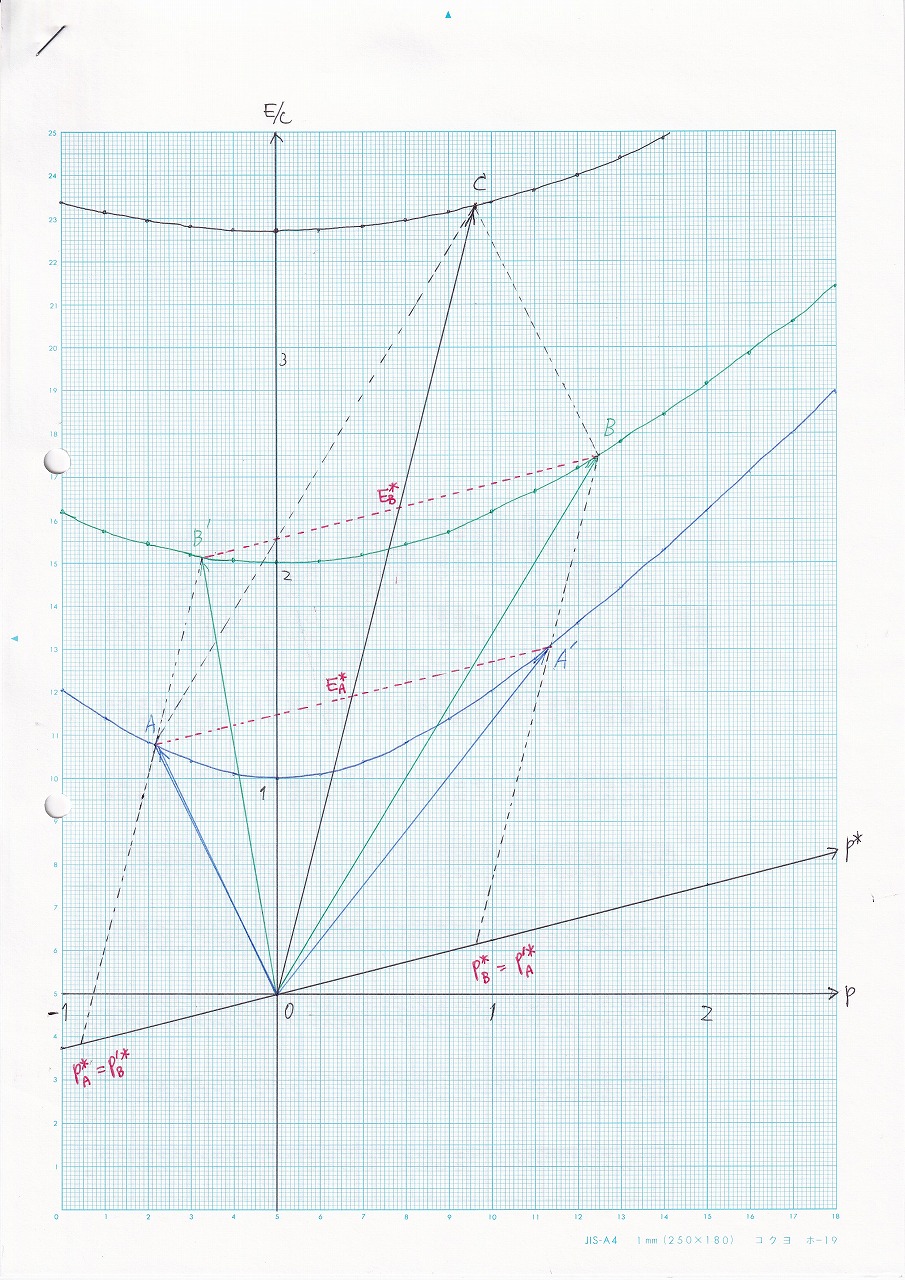
  図7.5～7.7
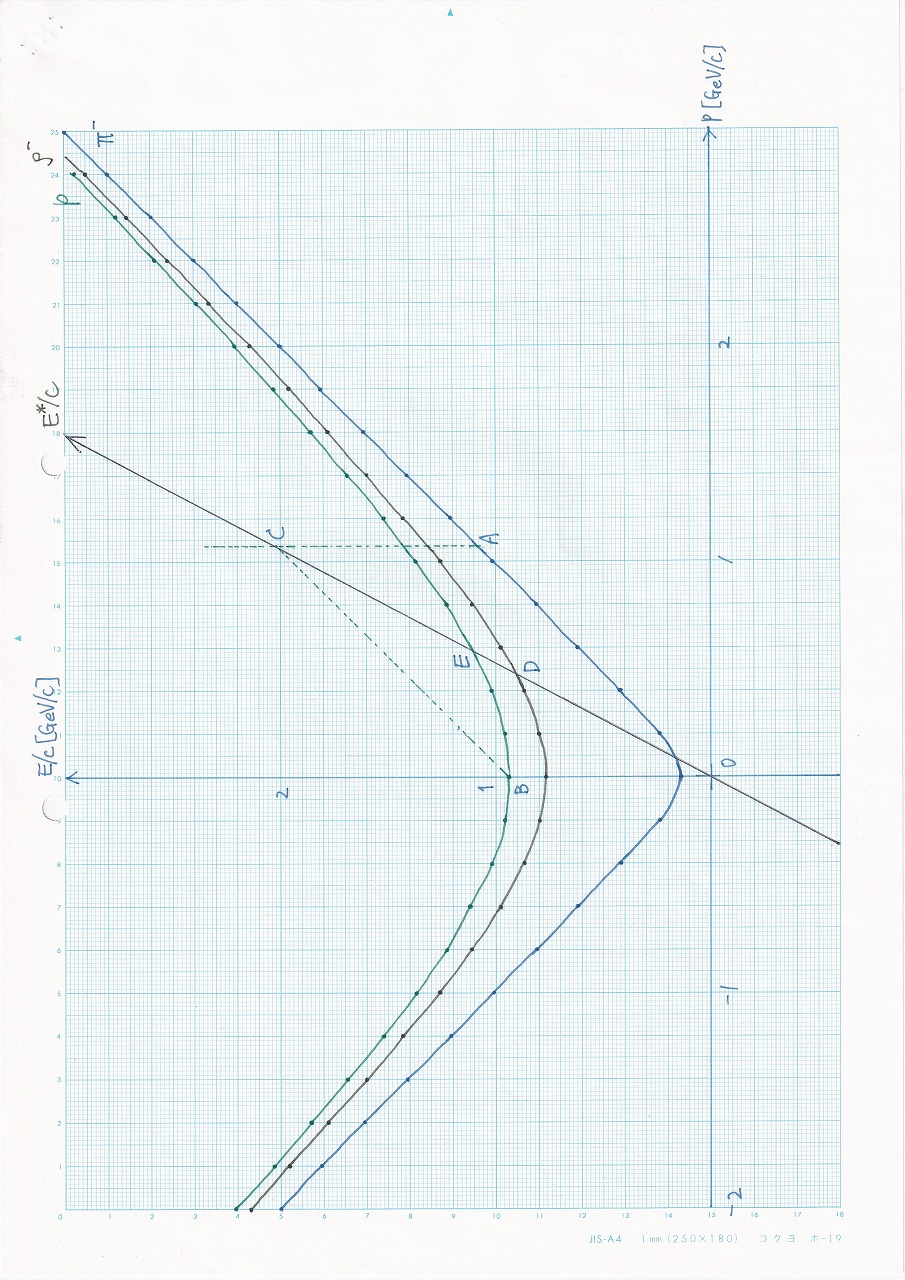  p150の例3	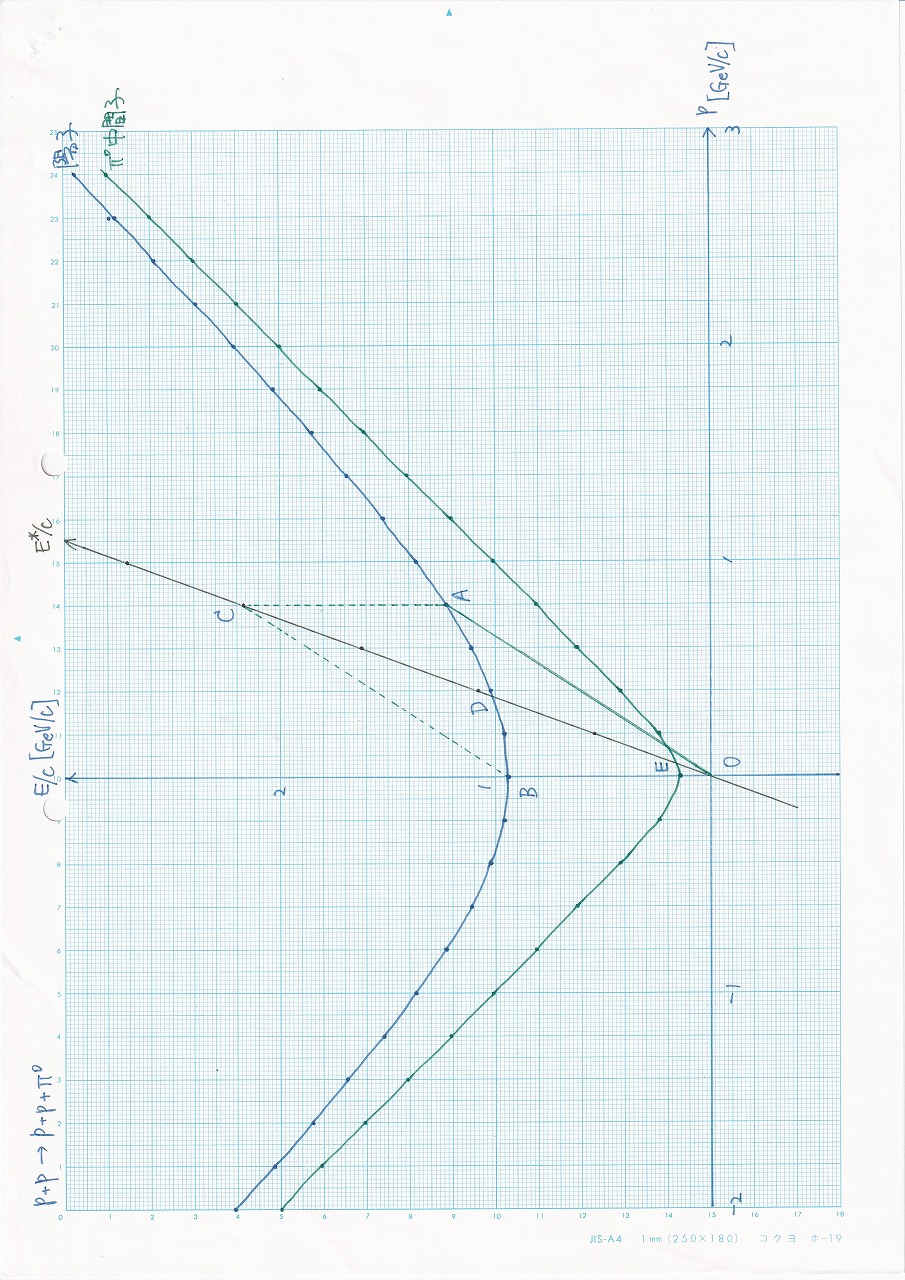p151の例
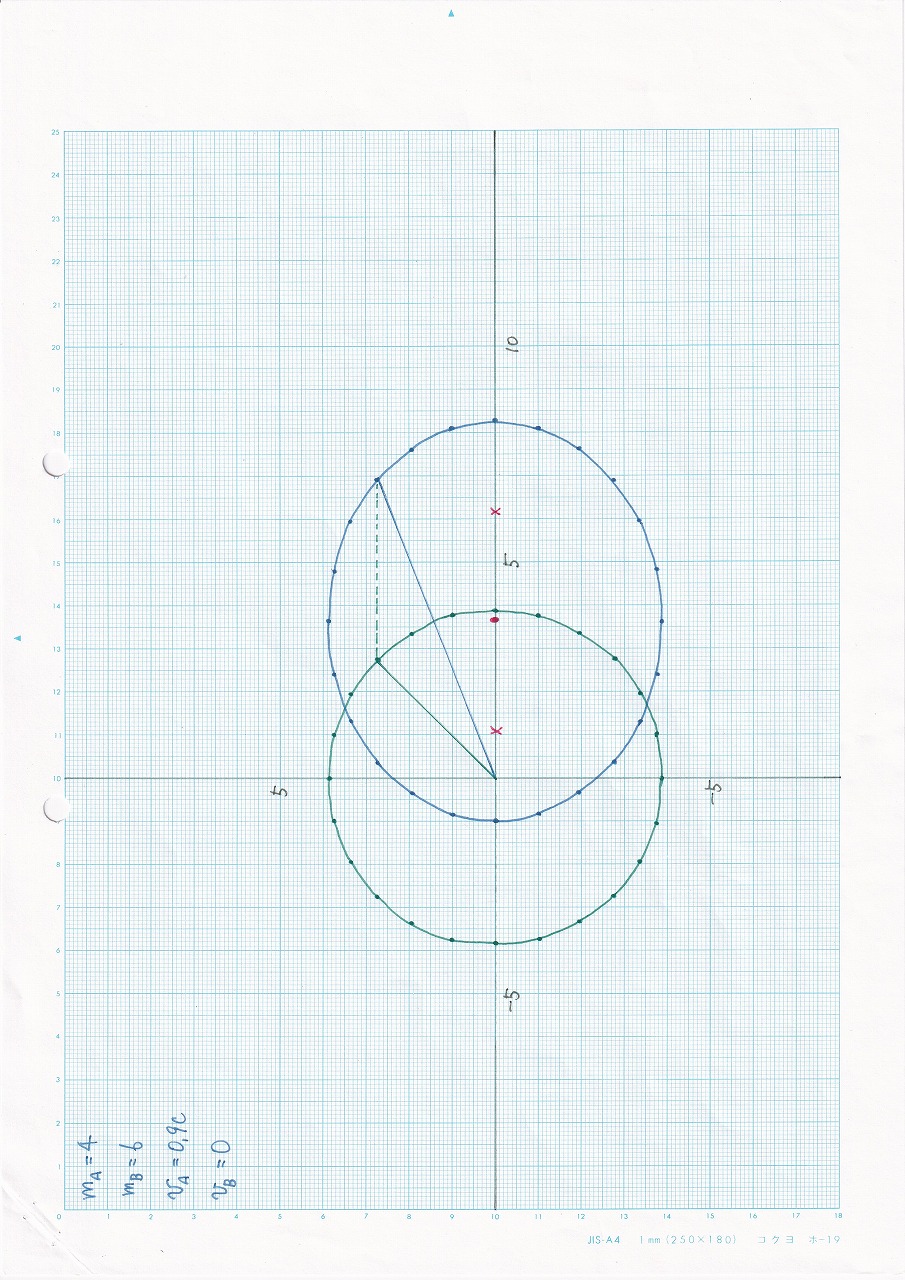  図7.13：vA=0.9c，vB=0，mA<mB	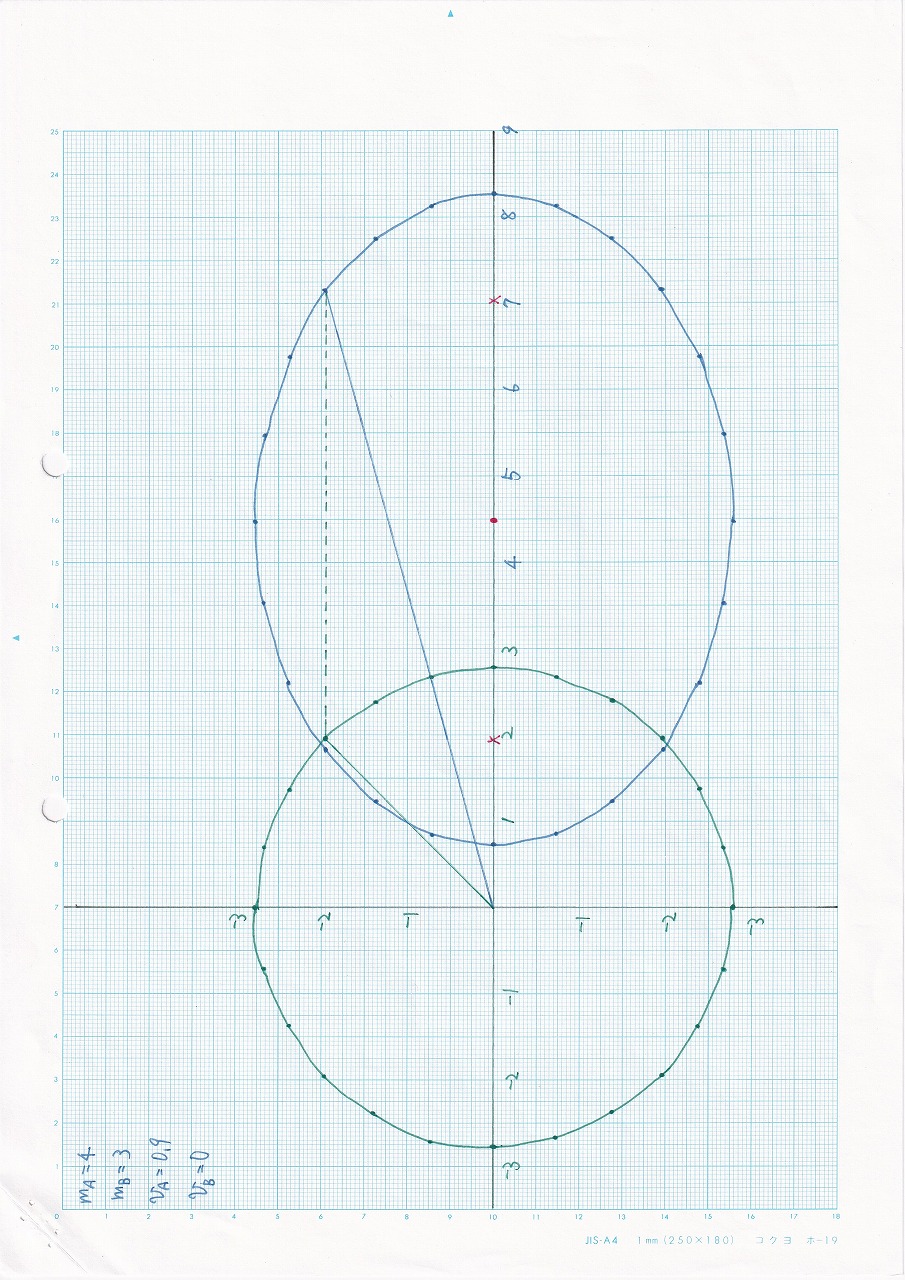図7.14：vA=0.9c，vB=0，mA>mB
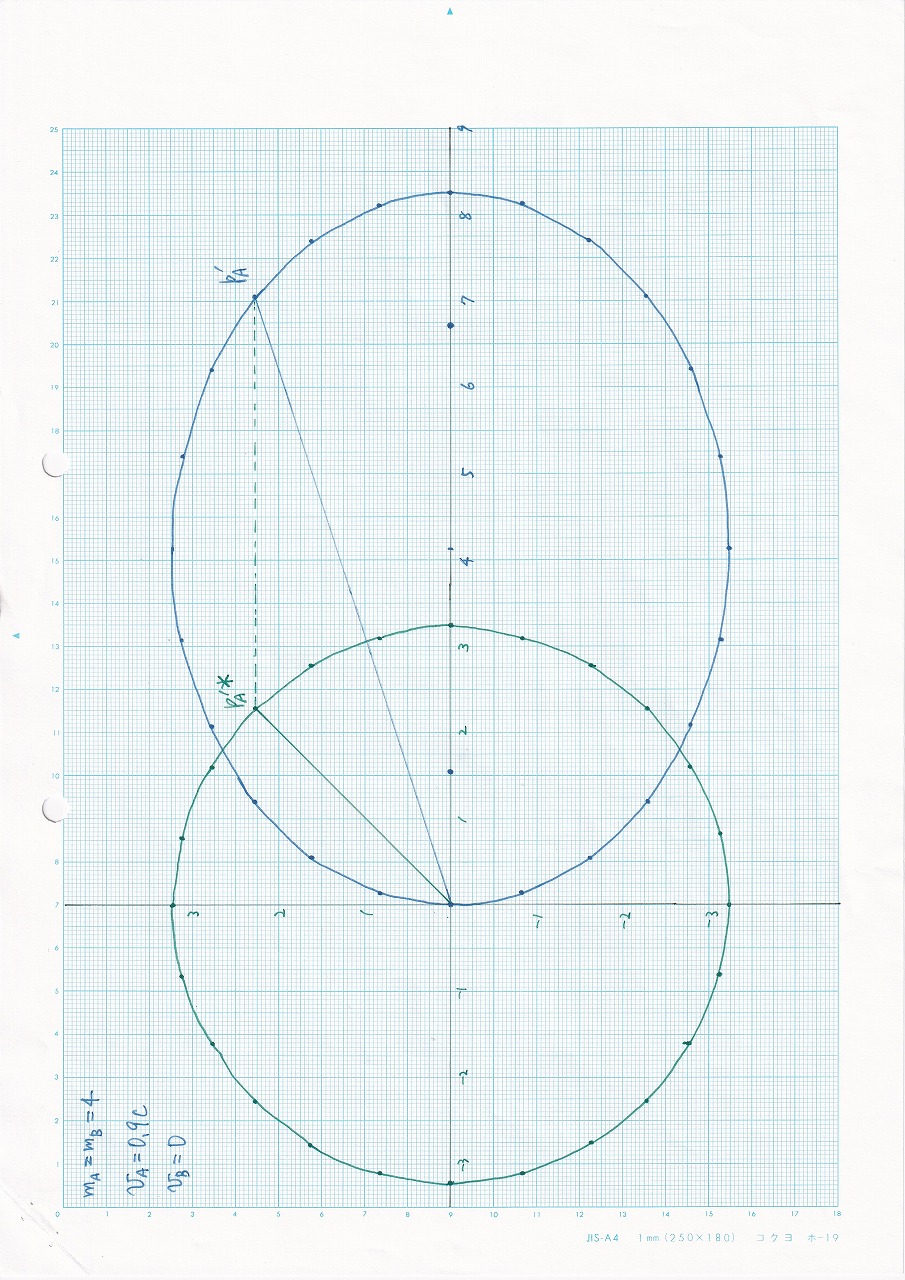  図7.16：vA=0.9c，vB=0，mA=mB	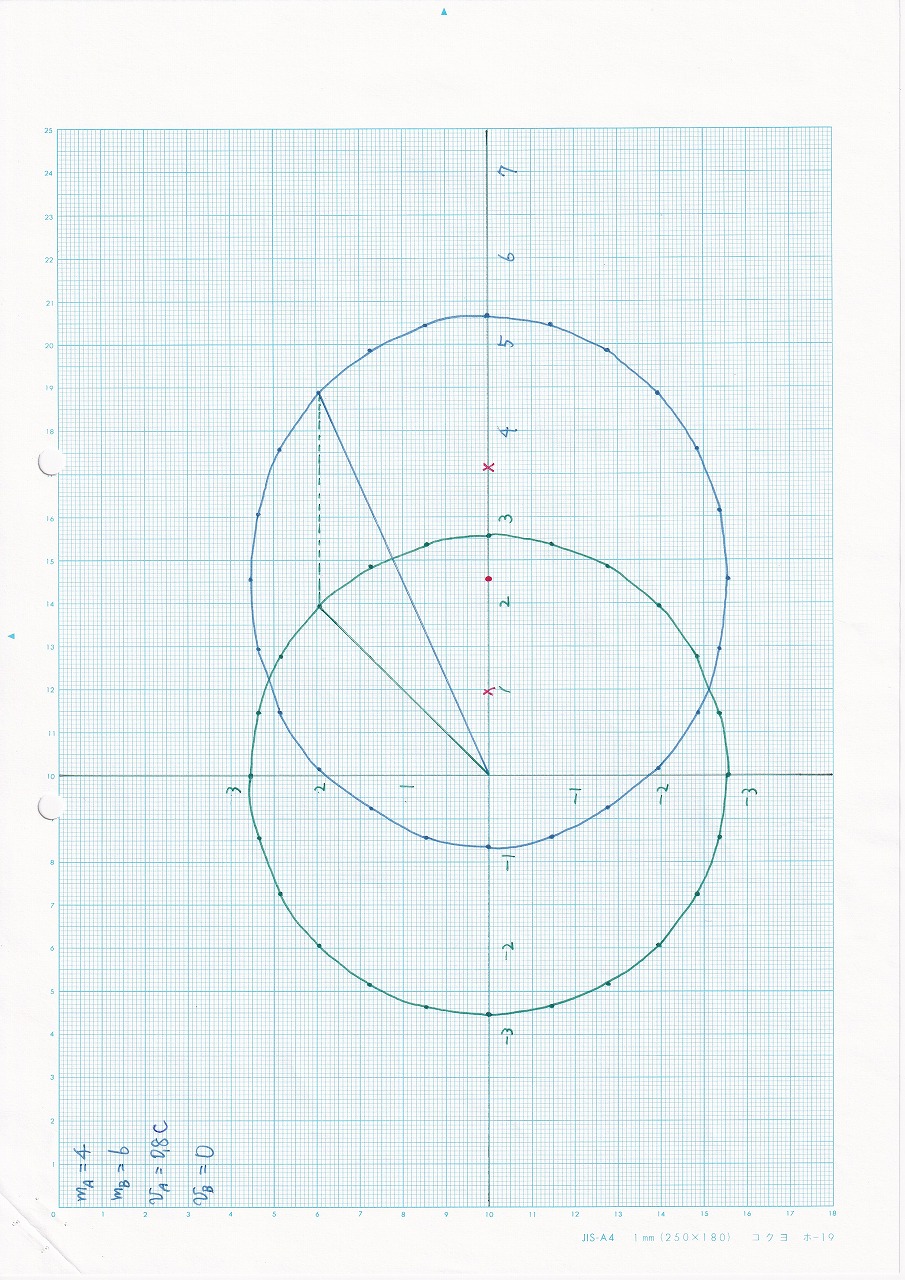なし：vA=0.8c，vB=0，mA<mB
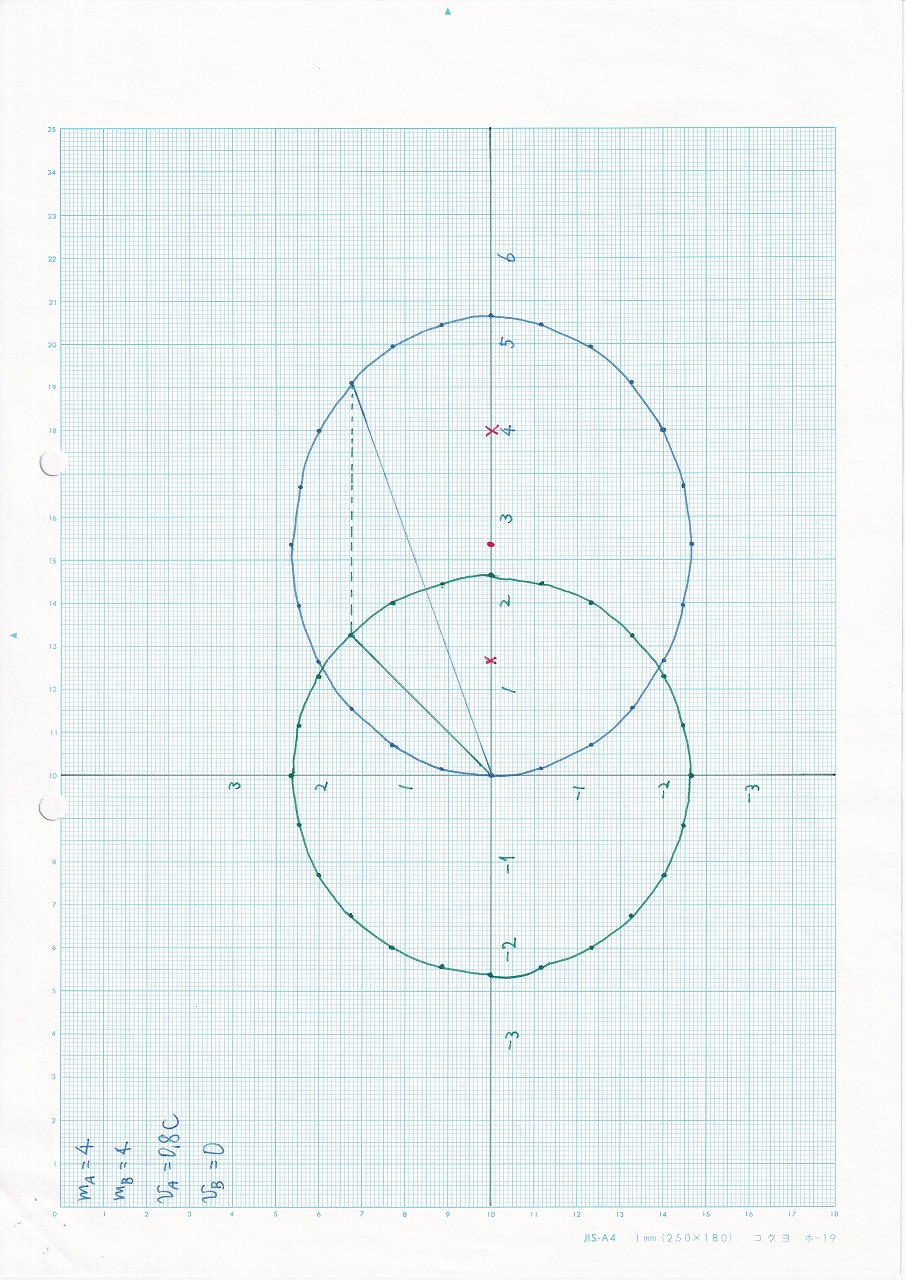  なし：vA=0.8c，vB=0，mA=mB	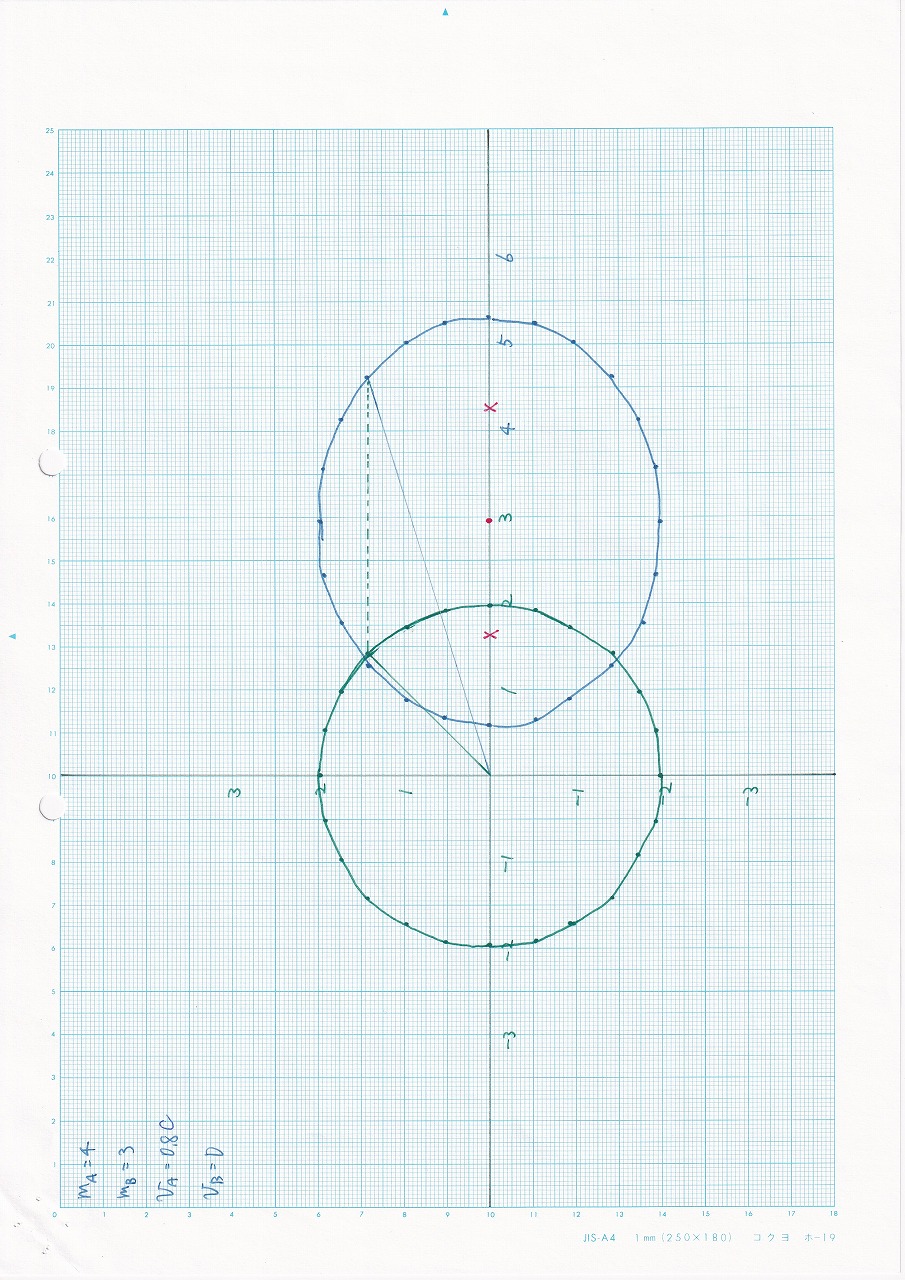なし：vA=0.8c，vB=0，mA>mB
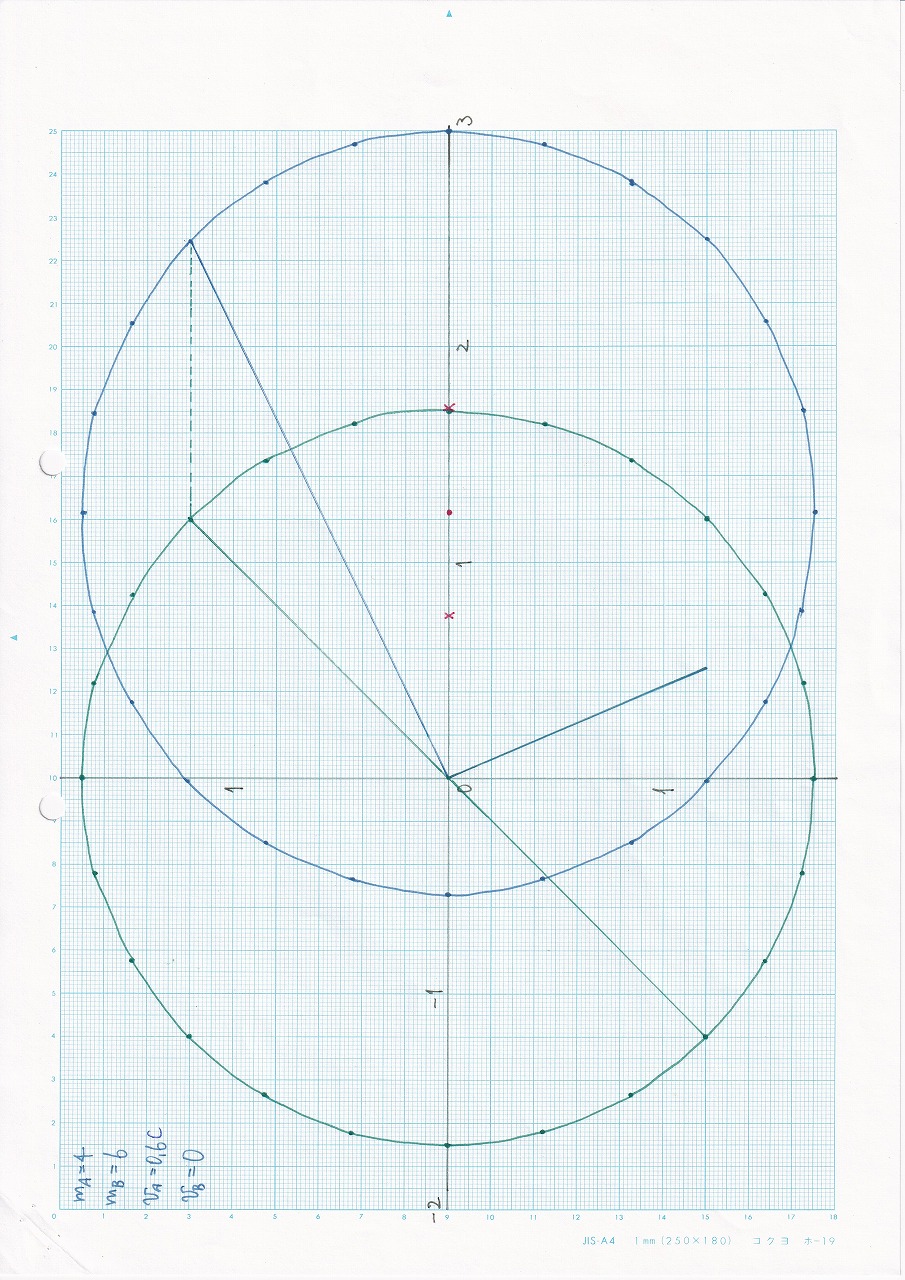  なし：vA=0.6c，vB=0，mA<mB	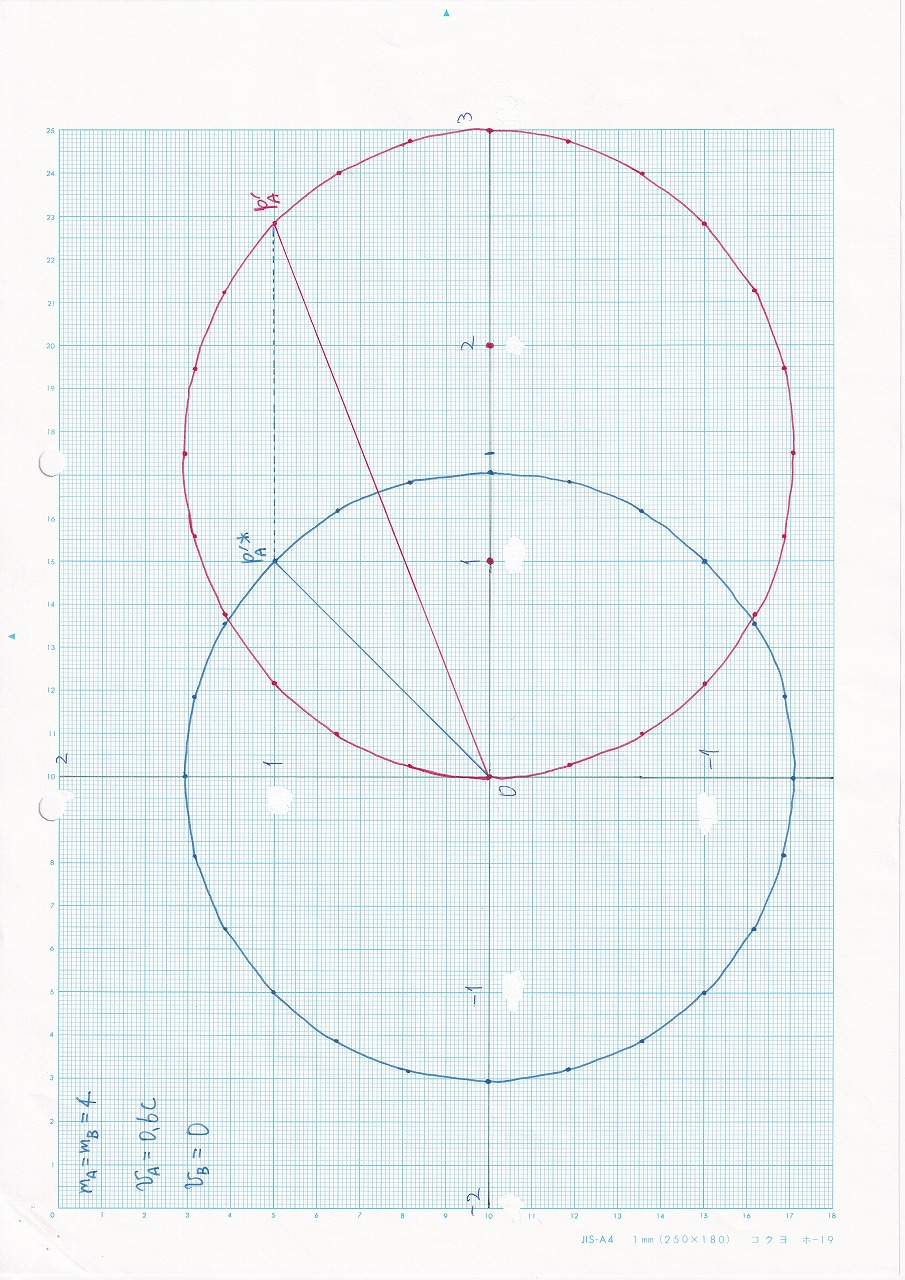図7.17：vA=0.6c，vB=0，mA=mB
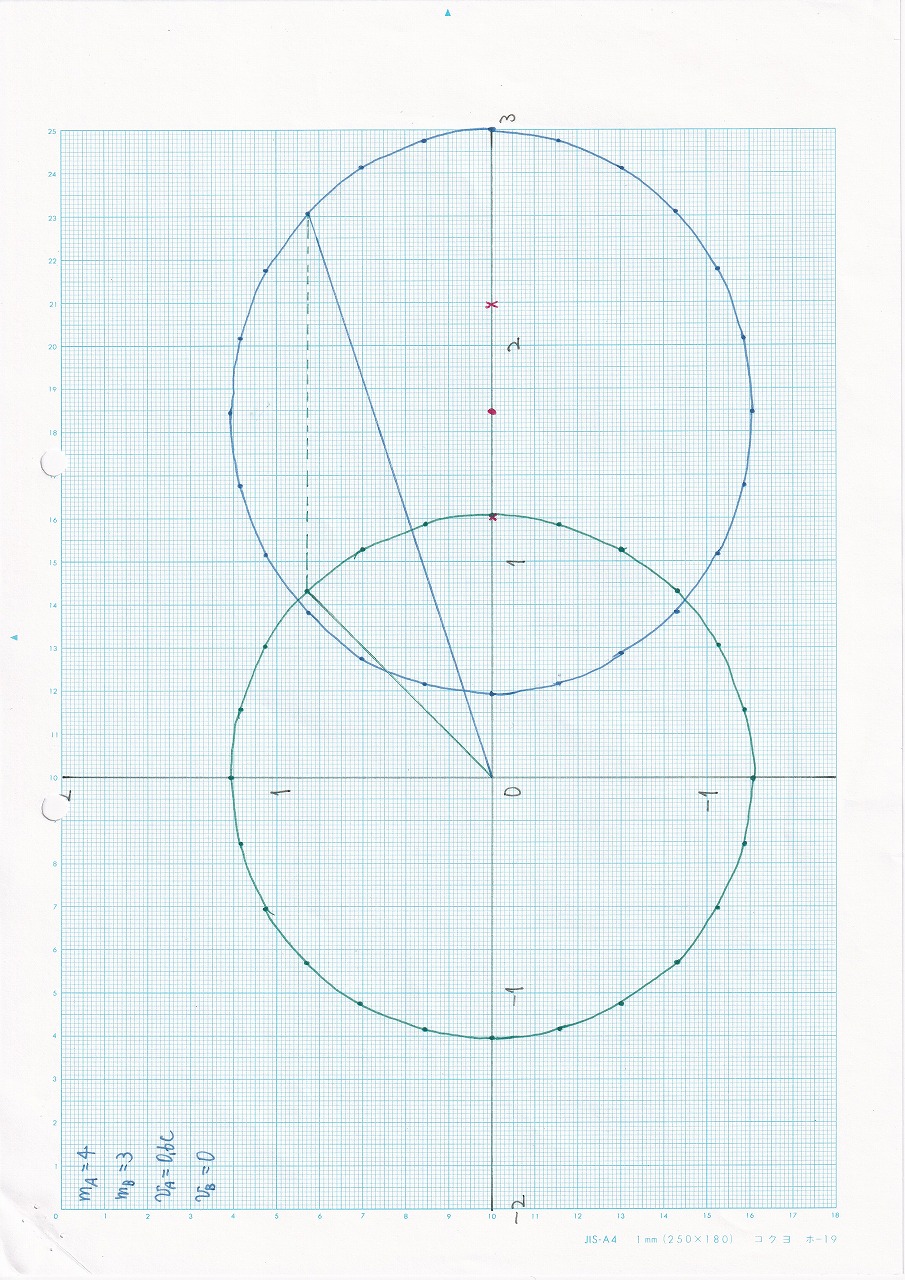  なし：vA=0.6c，vB=0，mA>mB	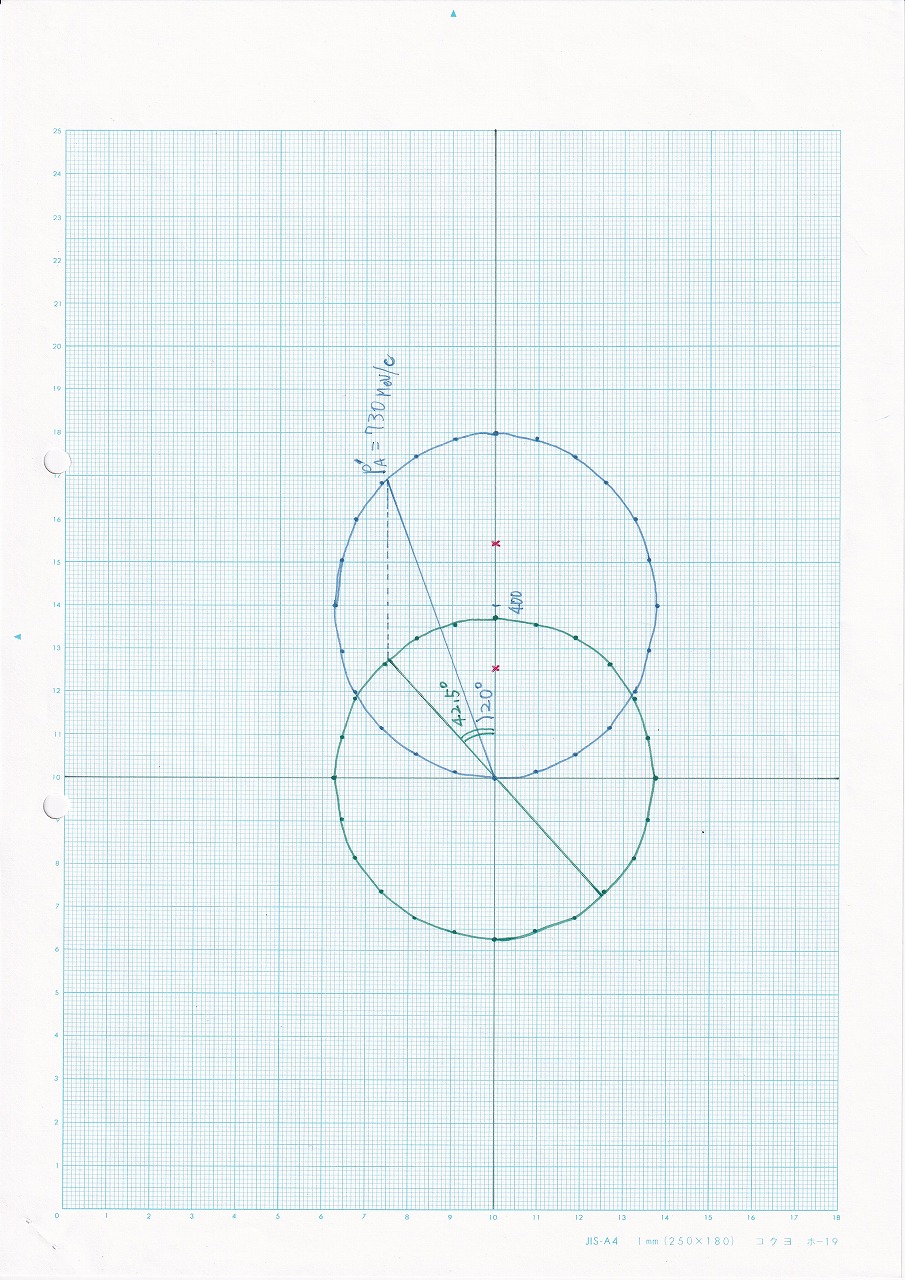p162例